题目内容
6.若正实数x,y满足x+y=1,则$\frac{y}{x}+\frac{4}{y}$的最小值是8.分析 根据题意,将$\frac{y}{x}+\frac{4}{y}$变形可得则$\frac{y}{x}+\frac{4}{y}$=$\frac{1-x}{x}$+$\frac{4}{y}$=$\frac{1}{x}$+$\frac{4}{y}$-1=(x+y)($\frac{1}{x}$+$\frac{4}{y}$)-1=(1+4+$\frac{y}{x}$+$\frac{4x}{y}$)-1=($\frac{y}{x}$+$\frac{4x}{y}$)+4,由基本不等式分析可得答案.
解答 解:根据题意,x,y满足x+y=1,
则$\frac{y}{x}+\frac{4}{y}$=$\frac{1-x}{x}$+$\frac{4}{y}$=$\frac{1}{x}$+$\frac{4}{y}$-1=(x+y)($\frac{1}{x}$+$\frac{4}{y}$)-1=(1+4+$\frac{y}{x}$+$\frac{4x}{y}$)-1=($\frac{y}{x}$+$\frac{4x}{y}$)+4≥2$\sqrt{\frac{y}{x}•\frac{4x}{y}}$+4=8,
即$\frac{y}{x}+\frac{4}{y}$的最小值是8;
故答案为:8.
点评 本题考查基本不等式的应用,关键是将$\frac{y}{x}+\frac{4}{y}$变形为($\frac{y}{x}$+$\frac{4x}{y}$)+4.

练习册系列答案
相关题目
14.已知a、b∈R,若3-4i3=$\frac{2-bi}{a+i}$,则a+b等于( )
| A. | -9 | B. | 5 | C. | 13 | D. | 9 |
1.已知非零向量$\overrightarrow{a}$,$\overrightarrow{b}$满足$\overrightarrow{a}$•$\overrightarrow{b}$=0,|$\overrightarrow{a}$|=3,且$\overrightarrow{a}$与$\overrightarrow{a}$+$\overrightarrow{b}$的夹角为$\frac{π}{4}$,则|$\overrightarrow{b}$|=( )
| A. | 6 | B. | 3$\sqrt{2}$ | C. | 2$\sqrt{2}$ | D. | 3 |
18.《九章算术》是我国古代内容极为丰富的数学名著,书中有如下问题:“今有五人五钱,令上二人所得与下三人等.问各得几何?”其意思为:“现有甲乙丙丁戊五人依次差值等额分五钱,要使甲乙两人所得的钱与丙丁戊三人所得的钱相等,问每人各得多少钱?”根据题意,乙得( )
| A. | $\frac{2}{3}$钱 | B. | $\frac{5}{6}$钱 | C. | 1钱 | D. | $\frac{7}{6}$钱 |
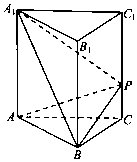
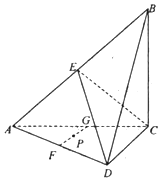 如图,在四面体ABCD中,平面ABC⊥平面ACD,E,F,G分别为AB,AD,AC的中点,AC=BC,∠ACD=90°.
如图,在四面体ABCD中,平面ABC⊥平面ACD,E,F,G分别为AB,AD,AC的中点,AC=BC,∠ACD=90°.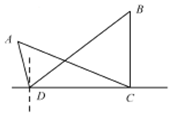 如图所示,为了测量A、B处岛屿的距离,小明在D处观测,A、B分别在D处的北偏西15°、北偏东45°方向,再往正东方向行驶40海里至C处,观测B在C处的正北方向,A在C处的北偏西60°方向,则A、B两处岛屿的距离为20$\sqrt{6}$海里.
如图所示,为了测量A、B处岛屿的距离,小明在D处观测,A、B分别在D处的北偏西15°、北偏东45°方向,再往正东方向行驶40海里至C处,观测B在C处的正北方向,A在C处的北偏西60°方向,则A、B两处岛屿的距离为20$\sqrt{6}$海里.