题目内容
2．如图，在正三棱柱ABC-A1B1C1中，已知AB=AA1=3，点P在棱CC1上，则三棱锥P-ABA1的体积为$\frac{9\sqrt{3}}{4}$．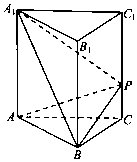
分析 点P到平面ABA1的距离即为△ABC的高，由此能求出三棱锥P-ABA1的体积．
解答 解：∵在正三棱柱ABC-A1B1C1中，AB=AA1=3，点P在棱CC1上，
∴点P到平面ABA1的距离即为△ABC的高，即为h=$\sqrt{{3}^{2}-（\frac{3}{2}）^{2}}$=$\frac{3\sqrt{3}}{2}$，
${S}_{△AB{A}_{1}}$=$\frac{1}{2}×3×3$=$\frac{9}{2}$，
三棱锥P-ABA1的体积为：V=$\frac{1}{3}×{S}_{△AB{A}_{1}}×h$=$\frac{1}{3}×\frac{9}{2}×\frac{3\sqrt{3}}{2}$=$\frac{9\sqrt{3}}{4}$．
故答案为：$\frac{9\sqrt{3}}{4}$．
点评 本题考查几何体的体积的求法，考查空间中线线、线面、面面的位置关系等基础知识，考查推理论证能力、运算求解能力、空间思维能力，考查数形结合、化归与转化思想，是中档题．
练习册系列答案
相关题目
13．已知集合A={x|0＜x＜2}，集合B={x|-1＜x＜1}，集合C={x|mx+1＞0}，若A∪B⊆C，则实数m的取值范围为（ ）
| A． | {m|-2≤m≤1} | B． | {m|-$\frac{1}{2}$≤m≤1} | C． | {m|-1≤m≤$\frac{1}{2}$} | D． | {m|-$\frac{1}{2}$≤m≤$\frac{1}{4}$} |
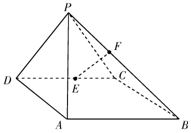如图，在四棱锥P-ABCD中，侧面PAD⊥底面ABCD，底面ABCD是平行四边形，∠ABC=45°，AD=AP=2，$AB=DP=2\sqrt{2}$，E为CD的中点，点F在线段PB上．
如图，圆O的弦AB，MN交于点C，且A为弧MN的中点，点D在弧BM上，若∠ACN=3∠ADB，求∠ADB的度数．