题目内容
已知实数x,y满足
.
(Ⅰ)求x+y的最大值与最小值;
(Ⅱ)求
的最大值与最小值.
|
(Ⅰ)求x+y的最大值与最小值;
(Ⅱ)求
| y |
| x+2 |
考点:简单线性规划
专题:不等式的解法及应用
分析:(1)作出不等式组所对应可得可行域,平移直线y=-x可得x+y的最大值与最小值;(2)转动直线可得
的最大值与最小值.
| y |
| x+2 |
解答:
解:(1)作出
所对应可得可行域(如图阴影),
作出直线y=-x,平移直线(红色虚线)知当直线过点A(0,
)时,截距最小,x+y取最小值
;
当直线过点B(3,2)时,截距最大,x+y取最大值5;
∴x+y的最大值为5,最小值为
;
(2)
表示可行域内的点与(-2,0)连线的斜率,
如图可知当直线(绿色虚线)过C(3,-1)时,
取最小值-
.
当直线过A(0,
)时,
取最大值
,

|
作出直线y=-x,平移直线(红色虚线)知当直线过点A(0,
| 1 |
| 2 |
| 1 |
| 2 |
当直线过点B(3,2)时,截距最大,x+y取最大值5;
∴x+y的最大值为5,最小值为
| 1 |
| 2 |
(2)
| y |
| x+2 |
如图可知当直线(绿色虚线)过C(3,-1)时,
| y |
| x+2 |
| 1 |
| 5 |
当直线过A(0,
| 1 |
| 2 |
| y |
| x+2 |
| 1 |
| 4 |

点评:本题考查线性规划,准确作图是解决问题的关键,属中档题.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
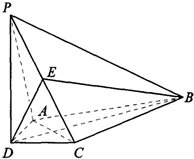 如图,在四棱锥P-ABCD中,PD⊥平面ABCD,AD⊥CD,DB平分∠ADC,E是PC的中点,AD=CD=1,
如图,在四棱锥P-ABCD中,PD⊥平面ABCD,AD⊥CD,DB平分∠ADC,E是PC的中点,AD=CD=1,