题目内容
17.在极坐标系下,知圆O:ρ=cosθ+sinθ和直线$l:ρsin({θ-\frac{π}{4}})=\frac{{\sqrt{2}}}{2}({ρ≥0,0≤θ≤2π})$.(1)求圆O与直线l的直角坐标方程;
(2)当θ∈(0,π)时,求圆O和直线l的公共点的极坐标.
分析 (1)圆O的极坐标方程化为ρ2=ρcosθ+ρsinθ,由此能求出圆O的直角坐标方程;直线l的极坐标方程化为ρsinθ-ρcosθ=1,由此能求出直线l的直角坐标方程.
(2)圆O与直线l的直角坐标方程联立,求出圆O与直线l的在直角坐标系下的公共点,由此能求出圆O和直线l的公共点的极坐标.
解答 解:(1)圆O:ρ=cosθ+sinθ,即ρ2=ρcosθ+ρsinθ,
故圆O的直角坐标方程为:x2+y2-x-y=0,
直线$l:ρsin({θ-\frac{π}{4}})=\frac{{\sqrt{2}}}{2}$,即ρsinθ-ρcosθ=1,
则直线的直角坐标方程为:x-y+1=0.
(2)由(1)知圆O与直线l的直角坐标方程,
将两方程联立得$\left\{{\begin{array}{l}{{x^2}+{y^2}-x-y=0}\\{x-y+1=0}\end{array}}\right.$,解得$\left\{{\begin{array}{l}{x=0}\\{y=1}\end{array}}\right.$.
即圆O与直线l的在直角坐标系下的公共点为(0,1),
转化为极坐标为$({1,\frac{π}{2}})$.
点评 本题考查直线与圆的直角坐标方程的求法,考查圆与直线的公共点的极坐标的求法,涉及到参数方程、普通方程、极坐标方程的互化等基础知识,考查推理论证能力、运算求解能力,考查化归与转化思想、函数与方程思想,是中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
1.把0,1,2三个数字组成四位数,每个数字至少使用一次,则这样的四位数的个数为( )
| A. | 18 | B. | 24 | C. | 27 | D. | 36 |
8.中心在原点,对称轴为坐标轴的双曲线C与圆O:x2+y2=10有公共点P(3,-1),且圆O在P点处的切线与双曲线C的一条渐近线平行,则该双曲线的实轴长为( )
| A. | $\frac{4\sqrt{5}}{3}$ | B. | 4$\sqrt{5}$ | C. | $\frac{8\sqrt{5}}{3}$ | D. | 8$\sqrt{5}$ |
5.如图,网格纸上小正方形的边长为1,粗线画出的是某多面体的三视图,则该多面体的体积为( )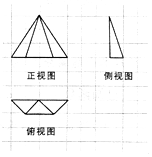

| A. | 3 | B. | 3$\sqrt{2}$ | C. | 9 | D. | 9$\sqrt{2}$ |
12.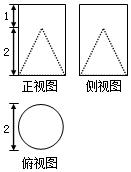 在一圆柱中挖去一圆锥所得的工艺部件的三视图如图所示,则此工艺部件的表面积为( )
在一圆柱中挖去一圆锥所得的工艺部件的三视图如图所示,则此工艺部件的表面积为( )
 在一圆柱中挖去一圆锥所得的工艺部件的三视图如图所示,则此工艺部件的表面积为( )
在一圆柱中挖去一圆锥所得的工艺部件的三视图如图所示,则此工艺部件的表面积为( )| A. | (7+$\sqrt{5}$)π | B. | (7+2$\sqrt{5}$)π | C. | (8+$\sqrt{5}$)π | D. | (8+2$\sqrt{5}$)π |
6.若关于x的不等式|x-1|+x≤a无解,则实数a的取值范围是( )
| A. | (-∞,1) | B. | (∞,1] | C. | (1,+∞) | D. | [1,+∞) |
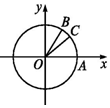 在如图所示的直角坐标系xOy中,点A,B是单位圆上的点,且A(1,0),∠AOB=$\frac{π}{3}$.现有一动点C在单位圆的劣弧$\widehat{AB}$上运动,设∠AOC=α.
在如图所示的直角坐标系xOy中,点A,B是单位圆上的点,且A(1,0),∠AOB=$\frac{π}{3}$.现有一动点C在单位圆的劣弧$\widehat{AB}$上运动,设∠AOC=α.