题目内容
已知集合Im={1,2,3,…n},Pm={
|m∈Im,k∈Im},求P7的元素个数.
| m | ||
|
考点:元素与集合关系的判断
专题:集合
分析:根据题意和集合Pm中元素的性质,对m进行分类讨论,再集合中元素的互异性求出P7的元素个数.
解答:
解:因为Im={1,2,3,…n},Pm={
|m∈Im,k∈Im},
所以I7={1,2,3,…,7},P7={
|m∈I7,k∈I7},
当m=1时,
可以是:1、
、
、
、…、
;
当m=2时,
可以是:2、
、
、1、…、
;
当m=3时,
可以是:3、
、
、
、…、
;
当m=4时,
可以是:4、
、
、2、…、
;
当m=5时,
可以是:5、
、
、
、…、
;
当m=6时,
可以是:6、
、
、3、…、
;
当m=7时,
可以是:7、
、
、
、…、
;
综上可得,重复的元素为1、2、3,
所以P7的元素个数是7×7-3=46.
| m | ||
|
所以I7={1,2,3,…,7},P7={
| m | ||
|
当m=1时,
| m | ||
|
| 1 | ||
|
| 1 | ||
|
| 1 |
| 2 |
| 1 | ||
|
当m=2时,
| m | ||
|
| 2 | ||
|
| 2 | ||
|
| 2 | ||
|
当m=3时,
| m | ||
|
| 3 | ||
|
| 3 | ||
|
| 3 |
| 2 |
| 3 | ||
|
当m=4时,
| m | ||
|
| 4 | ||
|
| 4 | ||
|
| 4 | ||
|
当m=5时,
| m | ||
|
| 5 | ||
|
| 5 | ||
|
| 5 |
| 2 |
| 5 | ||
|
当m=6时,
| m | ||
|
| 6 | ||
|
| 6 | ||
|
| 6 | ||
|
当m=7时,
| m | ||
|
| 7 | ||
|
| 7 | ||
|
| 7 |
| 2 |
| 7 | ||
|
综上可得,重复的元素为1、2、3,
所以P7的元素个数是7×7-3=46.
点评:本题考查集合元素的互异性,以及分类讨论的数学思想,属于中档题.

练习册系列答案
相关题目
若角α的终边在第二象限,则( )
| A、cosαtanα>0 |
| B、sinαtanα>0 |
| C、sinαcosα>0 |
| D、sinα+cosα>0 |
设变量x、y满足约束条件
,则z=2x×(
)y的最小值为( )
|
| 1 |
| 4 |
A、
| ||
B、
| ||
C、
| ||
D、
|
函数y=
+
的定义域为( )
| x+1 |
| 1 |
| x-1 |
| A、(-1,1) |
| B、[-1,1) |
| C、(-1,1)∪(1,+∞) |
| D、[-1,1)∪(1,+∞) |
把函数y=sin2x+
cos2x图象上所有点的横坐标缩短到原来的
倍,纵坐标不变,所得的图象解析式为( )
| 3 |
| 1 |
| 2 |
A、y=2sin(4x+
| ||
B、y=2sin(4x+
| ||
C、y=2sin(x+
| ||
D、y=2sin(x+
|
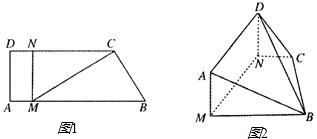 如图1,直角梯形ABCD中AB∥CD,∠ADC=90°,点M,N分别在线段AB,CD上,且MN⊥AB,BC=1,MB=2,∠CBM=60°,现将梯形ABCD沿MN折起,使DN⊥NC,如图2.
如图1,直角梯形ABCD中AB∥CD,∠ADC=90°,点M,N分别在线段AB,CD上,且MN⊥AB,BC=1,MB=2,∠CBM=60°,现将梯形ABCD沿MN折起,使DN⊥NC,如图2.