题目内容
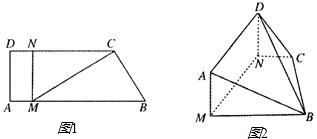 如图1,直角梯形ABCD中AB∥CD,∠ADC=90°,点M,N分别在线段AB,CD上,且MN⊥AB,BC=1,MB=2,∠CBM=60°,现将梯形ABCD沿MN折起,使DN⊥NC,如图2.
如图1,直角梯形ABCD中AB∥CD,∠ADC=90°,点M,N分别在线段AB,CD上,且MN⊥AB,BC=1,MB=2,∠CBM=60°,现将梯形ABCD沿MN折起,使DN⊥NC,如图2.(Ⅰ)求证:平面AMND⊥平面MNCB;
(Ⅱ)当直线DB与平面MNCB所成角的大小为30°时,求三棱锥C-DNB的体积.
考点:棱柱、棱锥、棱台的体积,平面与平面垂直的判定
专题:空间位置关系与距离,空间角
分析:(Ⅰ)由已知得DN⊥MN,又DN⊥NC,MN∩NC=N,从而DN⊥平面MNCB,由此能证明平面AMND⊥平面MNCB.
(Ⅱ)以N为原点,NM为x轴,NC为y轴,ND为z轴,建立空间直角坐标系,利用向量法能求出三棱锥C-DNB的体积.
(Ⅱ)以N为原点,NM为x轴,NC为y轴,ND为z轴,建立空间直角坐标系,利用向量法能求出三棱锥C-DNB的体积.
解答:
(Ⅰ)证明:∵直角梯形ABCD中AB∥CD,∠ADC=90°,
点M,N分别在线段AB,CD上,且MN⊥AB,
∴DN⊥MN,又DN⊥NC,MN∩NC=N,
∴DN⊥平面MNCB,
又DN?平面AMND,∴平面AMND⊥平面MNCB.
(Ⅱ)解:由(Ⅰ)知BM⊥平面MNCB,
∵直线DB与平面MNCB所成角的大小为30°,∴∠BDM=30°,
由已知得BM=2,CN=
,BC=1,BD=4,DM=2
,
MN=
,DN=
,BN=
,
以N为原点,NM为x轴,NC为y轴,ND为z轴,
建立空间直角坐标系,
则N(0,0,0),D(0,0,
),B(
,2,0),C(0,
,0),
=(
,2,0),
=(0,0,
),
=(0,
,0),
设平面NBD的法向量
=(x,y,z),
则
,取x=4
,得
=(4
,-3,0),
∴C到平面BDN的距离d=
=
=
,
S△BDN=
×DN×BN=
×
×
=
,
∴三棱锥C-DNB的体积V=
×S△BDN×d=
×
×
=
.

点M,N分别在线段AB,CD上,且MN⊥AB,
∴DN⊥MN,又DN⊥NC,MN∩NC=N,
∴DN⊥平面MNCB,
又DN?平面AMND,∴平面AMND⊥平面MNCB.
(Ⅱ)解:由(Ⅰ)知BM⊥平面MNCB,
∵直线DB与平面MNCB所成角的大小为30°,∴∠BDM=30°,
由已知得BM=2,CN=
| 3 |
| 2 |
| 3 |
MN=
| ||
| 2 |
3
| ||
| 2 |
| ||
| 2 |
以N为原点,NM为x轴,NC为y轴,ND为z轴,
建立空间直角坐标系,
则N(0,0,0),D(0,0,
3
| ||
| 2 |
| ||
| 2 |
| 3 |
| 2 |
| NB |
| ||
| 2 |
| ND |
3
| ||
| 2 |
| NC |
| 3 |
| 2 |
设平面NBD的法向量
| n |
则
|
| 3 |
| n |
| 3 |
∴C到平面BDN的距离d=
|
| ||||
|
|
|-
| ||
|
3
| ||
| 38 |
S△BDN=
| 1 |
| 2 |
| 1 |
| 2 |
3
| ||
| 2 |
| ||
| 2 |
3
| ||
| 8 |
∴三棱锥C-DNB的体积V=
| 1 |
| 3 |
| 1 |
| 3 |
3
| ||
| 8 |
3
| ||
| 38 |
3
| ||
| 304 |
点评:本题考查平面与平面垂直的证明,考查三棱锥的体积的求法,是中档题,解题时要注意空间思维能力的培养.

练习册系列答案
相关题目
