题目内容

10．已知某公司现有职员150人，其中中级管理人员30人，高级管理人员10人，要从公司抽取30个人进行身体健康检查，如果采用分层抽样的方法，则职员中“中级管理人员”和“高级管理人员”各应该抽取的人数为（　　）
A．8，2B．8，3C．6，3D．6，2

分析 利用要抽取的人数除以总人数，得到每个个体被抽到的概率，用概率乘以各个层次的人数，得到结果．

解答 解：∵公司现有职员150人，其中中级管理人员30人，高级管理人员10人，
∴从公司抽取30个人进行身体健康检查，每个个体被抽到的概率是$\frac{30}{150}$=$\frac{1}{5}$，
∴中级管理人员30×$\frac{1}{5}$=6人，
高级管理人员10×$\frac{1}{5}$=2人，
故选：D．

点评 本题考查分层抽样方法，解题的主要依据是每个个体被抽到的概率相等，主要是一些比较小的数字的运算，本题是一个基础题．

练习册系列答案
相关题目
20．已知集合A={x|m-1≤x≤2m+3}，函数f（x）=lg（-x2+2x+8）的定义域为B．
（1）当m=2时，求A∪B、（∁RA）∩B；
（2）若A∩B=A，求实数m的取值范围．
1．设F1，F2分别是双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$（a＞0，b＞0）的左、右焦点，若双曲线右支上存在一点P，使得$（\overrightarrow{OP}+\overrightarrow{O{F_2}}）•\overrightarrow{{F_2}P}=0$，其中O为坐标原点，且$|\overrightarrow{P{F_1}}|=3|\overrightarrow{P{F_2}}|$，则该双曲线的离心率为（　　）
A．$\sqrt{5}$B．$\sqrt{10}$C．$\frac{{\sqrt{10}}}{2}$D．$\frac{5}{2}$
18．将某班的60名学生编号为01，02，…，60，采用系统抽样方法抽取一个容量为5的样本，且随机抽得的一个号码为03，则剩下的四个号码依次是15，27，39，51．
5．斜率为$\sqrt{3}$的直线l经过抛物线y2=2px（p＞0）的焦点F，且交抛物线于A，B两点，若AB中点到抛物线准线的距离为4，则p的值为（　　）
A．1B．2C．3D．4
15．已知中心在原点，焦点在坐标轴上的椭圆E的方程为$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）它的离心率为$\frac{{\sqrt{3}}}{3}$，一个焦点是（-1，0），过直线x=3上一点M引椭圆E的两条切线，切点分别是A和B．
（Ⅰ）求椭圆E的方程；
（Ⅱ）若在椭圆E：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）上的点（x0，y0）处的切线方程是$\frac{{x}_{0}x}{{a}^{2}}$+$\frac{{y}_{0}y}{{b}^{2}}$=1．求证：直线AB恒过定点，并求出定点的坐标；
（Ⅲ）记点C为（Ⅱ）中直线AB恒过的定点，问是否存在实数λ，使得$|{\overrightarrow{AC}}|+|{\overrightarrow{BC}}|=λ|{\overrightarrow{AC}}|•|{\overrightarrow{BC}}|$成立，若成立求出λ的值，若不存在，请说明理由．
2．集合A={x||x-1|＜2}，B={x|$\frac{1}{9}$＜3x＜9}，则A∩B=（　　）
A．（-1，3）B．（-1，2）C．（-2，2）D．（-2，3）
19．如图是某几何体的三视图且a=b，则该几何体主视图的面积为（　　）
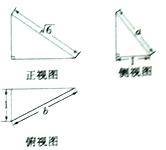
A．$\sqrt{6}$B．$\frac{3}{2}$C．$\frac{{\sqrt{3}}}{2}$D．$\frac{{\sqrt{15}}}{2}$
20．若函数f（x）=2x+x-4的零点x0∈（a，b），且b-a=1，a，b∈N，则a+b=3．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网