题目内容
7.已知$sin(α+\frac{π}{5})=\frac{{\sqrt{3}}}{3}$,则$cos(2α+\frac{2π}{5})$=( )| A. | $\frac{1}{3}$ | B. | $\frac{{\sqrt{3}}}{3}$ | C. | $\frac{2}{3}$ | D. | $\frac{{\sqrt{3}}}{2}$ |
分析 利用二倍角公式求解即可.
解答 解:由题意:$sin(α+\frac{π}{5})=\frac{{\sqrt{3}}}{3}$,
∴$cos(2α+\frac{2π}{5})$=cos2($α+\frac{π}{5}$)=1-2sin2($α+\frac{π}{5}$)=1-2×($\frac{\sqrt{3}}{3}$)2=$\frac{1}{3}$.
故选A.
点评 本题考查了二倍角公式的运用!构造思想.属于比较基础的题.

练习册系列答案
相关题目
18.抛物线y2=2x的准线方程为( )
| A. | x=1 | B. | x=$\frac{1}{2}$ | C. | x=-1 | D. | x=-$\frac{1}{2}$ |
15.M是抛物线C:y2=2px(p>0)上一点,F是抛物线C的焦点,O为坐标原点,若|MF|=p,K是抛物线C准线与x轴的交点,则∠MKO=( )
| A. | 15° | B. | 30° | C. | 45° | D. | 60° |
12.已知x与y之间的一组数据:
已求得关于y与x的线性回归方程$\stackrel{∧}{y}$=1.2x+0.55,则a的值为2.15.
| x | 0 | 2 | 4 | 6 |
| y | a | 3 | 5 | 3a |
19.执行如图所示的程序框图,若输入n=2017,输出S的值为0,则f(x)的解析式可以是( )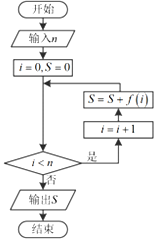

| A. | $f(x)=sin(\frac{π}{3}x)$ | B. | $f(x)=sin(\frac{π}{2}x)$ | C. | $f(x)=cos(\frac{π}{3}x)$ | D. | $f(x)=cos(\frac{π}{2}x)$ |
16.过点P在双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1的右支上,其左、右焦点分别为F1,F2,PF1的垂直平分线过F2,且原点到直线PF1的距离恰好等于双曲线的实半轴长,则该双曲线的离心率为( )
| A. | $\frac{7}{3}$ | B. | $\frac{5}{3}$ | C. | $\frac{5}{4}$ | D. | $\frac{7}{4}$ |