题目内容
9.已知$\overrightarrow{a}$=(-1,2),$\overrightarrow{b}$=(x,3),且$\overrightarrow{a}$⊥$\overrightarrow{b}$,则|$\overrightarrow{b}$|=( )| A. | 3 | B. | 5 | C. | $\sqrt{5}$ | D. | 3$\sqrt{5}$ |
分析 由向量垂直的性质得$\overrightarrow{a}•\overrightarrow{b}$=-x+6=0,求出$\overrightarrow{b}$=(6,3),由此能求出|$\overrightarrow{b}$|.
解答 解:∵$\overrightarrow{a}$=(-1,2),$\overrightarrow{b}$=(x,3),且$\overrightarrow{a}$⊥$\overrightarrow{b}$,
∴$\overrightarrow{a}•\overrightarrow{b}$=-x+6=0,
解得x=6.
∴$\overrightarrow{b}$=(6,3),
∴|$\overrightarrow{b}$|=$\sqrt{36+9}$=3$\sqrt{5}$.
故选:D.
点评 本题考查向量的模的求法,是基础题,解题时要认真审题,注意平面向量坐标运算法则的合理运用.

练习册系列答案
相关题目
18.抛物线y2=2x的准线方程为( )
| A. | x=1 | B. | x=$\frac{1}{2}$ | C. | x=-1 | D. | x=-$\frac{1}{2}$ |
19.执行如图所示的程序框图,若输入n=2017,输出S的值为0,则f(x)的解析式可以是( )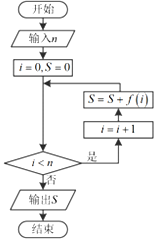

| A. | $f(x)=sin(\frac{π}{3}x)$ | B. | $f(x)=sin(\frac{π}{2}x)$ | C. | $f(x)=cos(\frac{π}{3}x)$ | D. | $f(x)=cos(\frac{π}{2}x)$ |