题目内容
2.若不等式n2-n(λ+1)+7≥λ,对一切n∈N*恒成立,则实数λ的取值范围( )| A. | λ≤3 | B. | λ≤4 | C. | 2≤λ≤3 | D. | 3≤λ≤4 |
分析 推导出n2-n+7≥λ(n+1),从而λ≤$\frac{{n}^{2}-n+7}{n+1}$对一切n∈N*恒成立.由此利用基本不等式能求出实数λ的取值范围.
解答 解:∵不等式n2-n(λ+1)+7≥λ,对一切n∈N*恒成立,
∴n2-n+7≥λ(n+1),
∵n∈N*,∴λ≤$\frac{{n}^{2}-n+7}{n+1}$对一切n∈N*恒成立.
而$\frac{{n}^{2}-n+7}{n+1}$=$\frac{(n+1)^{2}-3(n+1)+9}{n+1}$=(n+1)+$\frac{9}{n+1}$-3≥$2\sqrt{(n+1)•\frac{9}{n+1}}$-3=3,
当且仅当n+1=$\frac{9}{n+1}$,即=2时等号成立,
∴n≤3.
故选:A.
点评 本题考查实数的取值范围的求法,涉及到数列、均值不等式等基础知识,考查推理论证能力、运算求解能力,考查化归与转化思想、函数与方程思想,是中档题.

练习册系列答案
相关题目
13.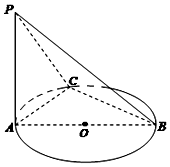 如图,AB是⊙O的直径,PA垂直于⊙O所在平面,C是圆周上不同于A,B两点的任意一点,且AB=2,$PA=BC=\sqrt{3}$,则直线PC与底面ABC所成角的大小为( )
如图,AB是⊙O的直径,PA垂直于⊙O所在平面,C是圆周上不同于A,B两点的任意一点,且AB=2,$PA=BC=\sqrt{3}$,则直线PC与底面ABC所成角的大小为( )
 如图,AB是⊙O的直径,PA垂直于⊙O所在平面,C是圆周上不同于A,B两点的任意一点,且AB=2,$PA=BC=\sqrt{3}$,则直线PC与底面ABC所成角的大小为( )
如图,AB是⊙O的直径,PA垂直于⊙O所在平面,C是圆周上不同于A,B两点的任意一点,且AB=2,$PA=BC=\sqrt{3}$,则直线PC与底面ABC所成角的大小为( )| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
7.$若f(n)=tan\frac{nπ}{3},(n∈{N^*}),则f(1)+f(2)+…+f(2017)$=( )
| A. | $-\sqrt{3}$ | B. | $\sqrt{3}$ | C. | 0 | D. | $-2\sqrt{3}$ |
18.直线x+2y=m(m>0)与⊙O:x2+y2=5交于A,B两点,若|${\overrightarrow{OA}$+$\overrightarrow{OB}}$|>2|${\overrightarrow{AB}}$|,则m的取值范围是( )
| A. | $({\sqrt{5},2\sqrt{5}})$ | B. | $({2\sqrt{5},5})$ | C. | $({\sqrt{5},5})$ | D. | $({2,\sqrt{5}})$ |
19.某几何体的三视图如图所示,则该几何体的体积为( )
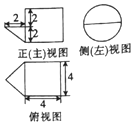

| A. | 6π | B. | $\frac{46}{3}$π | C. | 18π | D. | $\frac{52}{3}$π |