题目内容
若向量
、
满足|
|=1，|
|=2，且
与
的夹角为
，则
•（
+
）= ．
| a |
| b |
| a |
| b |
| a |
| b |
| π |
| 3 |
| a |
| a |
| b |
考点：平面向量数量积的运算
专题：平面向量及应用
分析：由题意可得可得
•
=1×2×cos
=1，再根据
•（
+
）=
2+
•
，求得结果．
| a |
| b |
| π |
| 3 |
| a |
| a |
| b |
| a |
| a |
| b |
解答：
解：由向量
、
满足|
|=1，|
|=2，且
与
的夹角为
，可得
•
=1×2×cos
=1，
则
•（
+
）=
2+
•
=1+1=2，
故答案为：2．
| a |
| b |
| a |
| b |
| a |
| b |
| π |
| 3 |
| a |
| b |
| π |
| 3 |
则
| a |
| a |
| b |
| a |
| a |
| b |
故答案为：2．
点评：本题主要考查两个向量的数量积的定义，两个向量的数量积公式的应用，属于基础题．
练习册系列答案
相关题目
复数z=
的共轭复数的虚部为（ ）
| 4+3i |
| 2-i |
| A、-2 | B、-2i | C、2 | D、2i |
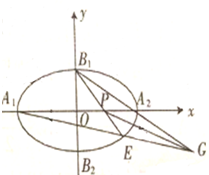已知焦点在x轴上的椭圆C的短轴长为2，离心率为
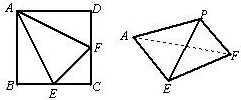正方形ABCD的边长为1，E、F分别为BC、CD的中点，沿AE、EF、AF折成四面体则四面体PAEF使B、C、D三点重合于P，则P到面AEF的距离为