题目内容
已知定义在(0,
)上的函数f(x),f′(x)为其导函数,且f(x)<f′(x)•tanx恒成立,则( )
| π |
| 2 |
A、
| ||||||||
B、
| ||||||||
C、
| ||||||||
D、f(1)<2f(
|
考点:导数在最大值、最小值问题中的应用
专题:计算题,函数的性质及应用,导数的综合应用
分析:把给出的等式变形得到f′(x)sinx-f(x)cosx>0,由此联想构造辅助函数g(x)=
,由其导函数的符号得到其在(0,
)上为增函数,则g(
)<g(
)<g(1)<g(
),整理后即可得到答案.
| f(x) |
| sinx |
| π |
| 2 |
| π |
| 6 |
| π |
| 4 |
| π |
| 3 |
解答:
解:解:因为x∈(0,
),所以sinx>0,cosx>0,
由f(x)<f′(x)tanx,得f(x)cosx<f′(x)sinx,
即f′(x)sinx-f(x)cosx>0.
令g(x)=
,x∈(0,
),则g′(x)=
>0.
所以函数g(x)=
在x∈(0,
)上为增函数,
则g(
)<g(
)<g(1)<g(
),即
<
<
<
,
对照选项,A.应为
f(
)>
f(
),C.应为
f(
)<f(
),
D.应为f(1)2f(
)sin1,B正确.
故选B.
| π |
| 2 |
由f(x)<f′(x)tanx,得f(x)cosx<f′(x)sinx,
即f′(x)sinx-f(x)cosx>0.
令g(x)=
| f(x) |
| sinx |
| π |
| 2 |
| f′(x)sinx-f(x)cosx |
| sin2x |
所以函数g(x)=
| f(x) |
| sinx |
| π |
| 2 |
则g(
| π |
| 6 |
| π |
| 4 |
| π |
| 3 |
f(
| ||
sin
|
f(
| ||
sin
|
| f(1) |
| sin1 |
f(
| ||
sin
|
对照选项,A.应为
| 2 |
| π |
| 3 |
| 3 |
| π |
| 4 |
| 2 |
| π |
| 6 |
| π |
| 4 |
D.应为f(1)2f(
| π |
| 6 |
故选B.
点评:本题考查了导数的运算法则,考查了利用函数导函数的符号判断函数的单调性,考查了函数构造法,属中档题型.

练习册系列答案
相关题目
若点N在直线1上,直线l又在平面α内,则点N,直线l与平面α之间的关系可记作( )
| A、N∈l∈α |
| B、N∈l?α |
| C、N?l?α |
| D、N?l∈α |
下列有关命题叙述错误的是( )
| A、已知集合A={1,4,2x},B={1,x2},若B⊆A,则x=0,或-2 |
| B、若“p或q”为假命题,则p,q均为假命题 |
| C、对于命题p:?x2>y2,x>y,则命题?p:?x2≤y2,x≤y |
| D、命题“若x2-3x+2=0,则x=1”的逆否命题为“若x≠1,则x2-3x+2≠0” |
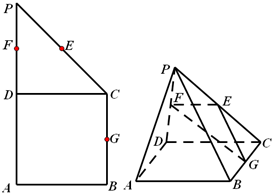 如图,在直角梯形ABCP中,BC∥AP,AB⊥BC,CD⊥AP,AD=CD=PD,E,F,G分别为线段PC,PD,BC的中点,现将△PDC折起,使点P∉平面ABCD.求证:PA∥面EFG.
如图,在直角梯形ABCP中,BC∥AP,AB⊥BC,CD⊥AP,AD=CD=PD,E,F,G分别为线段PC,PD,BC的中点,现将△PDC折起,使点P∉平面ABCD.求证:PA∥面EFG.