题目内容
已知:正四棱锥S-ABCD的棱长均为13,E,F分别是SA,BD上的点,且SE:EA=BF:FD=5:8.
(1)求证:EF∥平面SBC;
(2)求四棱锥S-ABCD的体积.
(1)求证:EF∥平面SBC;
(2)求四棱锥S-ABCD的体积.
考点:直线与平面平行的判定,棱柱、棱锥、棱台的体积
专题:空间位置关系与距离
分析:(1)如图所示,取点G,使BG:GA=5:8,EG∥SB,GF∥BC,得到平面EFG∥平面SBC,问题得以证明
(2)如图,连接AC,BD相交于点O,连接SO,可以得到SO是正四棱锥S-ABCD的高,再根据棱锥的体积公式计算即可
(2)如图,连接AC,BD相交于点O,连接SO,可以得到SO是正四棱锥S-ABCD的高,再根据棱锥的体积公式计算即可
解答:
 解:(1)证明:如图所示,取点G,使BG:GA=5:8.
解:(1)证明:如图所示,取点G,使BG:GA=5:8.
∵SE:EA=BF:FD=5:8.
∴EG∥SB,GF∥AD,
∵底面ABCD的为正方形,
∴AD∥BC,
∴GF∥BC,
∵EG∩GF=G,SB∩BC=C,EG,GF?平面EFG,SB,BC?平面SBC,
∴平面EFG∥平面SBC,
∵EF?平面EFG,EF?平面SBC,
∴EF∥平面SBC
(2)如图,连接AC,BD相交于点O,连接SO,
∴O点AC,BD的中点,
∵SA=SB=SC=SD,
∴SO⊥AC,SO⊥BD,
∴SO⊥底面ABCD,
即SO是正四棱锥S-ABCD的高,
∵正四棱锥S-ABCD的棱长均为13,
∴AO=
AC=
=
,
∴SO=
=
,
∵S底面ABCD=AB•BC=13×13=169,
∴V四棱锥S-ABCD=
×169×
=
 解:(1)证明:如图所示,取点G,使BG:GA=5:8.
解:(1)证明:如图所示,取点G,使BG:GA=5:8.∵SE:EA=BF:FD=5:8.
∴EG∥SB,GF∥AD,
∵底面ABCD的为正方形,
∴AD∥BC,
∴GF∥BC,
∵EG∩GF=G,SB∩BC=C,EG,GF?平面EFG,SB,BC?平面SBC,
∴平面EFG∥平面SBC,

∵EF?平面EFG,EF?平面SBC,
∴EF∥平面SBC
(2)如图,连接AC,BD相交于点O,连接SO,
∴O点AC,BD的中点,
∵SA=SB=SC=SD,
∴SO⊥AC,SO⊥BD,
∴SO⊥底面ABCD,
即SO是正四棱锥S-ABCD的高,
∵正四棱锥S-ABCD的棱长均为13,
∴AO=
| 1 |
| 2 |
| 1 |
| 2 |
| AB2+BC2 |
13
| ||
| 2 |
∴SO=
| SA2-AO2 |
13
| ||
| 2 |
2197
| ||
| 6 |
∵S底面ABCD=AB•BC=13×13=169,
∴V四棱锥S-ABCD=
| 1 |
| 3 |
13
| ||
| 2 |
2197
| ||
| 6 |
点评:本题考查线面平行的证明,体积的计算,解题时要认真审题,注意空间思维能力的培养,属于中档题

练习册系列答案
相关题目
圆x2+y2-4y=0的圆心坐标和半径分别为( )
| A、(0,2),2 |
| B、(0,-2),2 |
| C、(-2,0),2 |
| D、(2,0),2 |
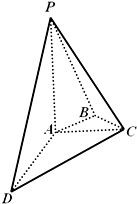 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,AC⊥AD,AB⊥BC,∠BAC=45°,PA=AD=2,AC=1.
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,AC⊥AD,AB⊥BC,∠BAC=45°,PA=AD=2,AC=1.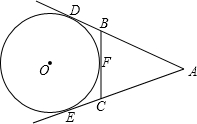 如图:AE、AD、BC分别切⊙O于E、D、F,若AD=18,则△ABC的周长为
如图:AE、AD、BC分别切⊙O于E、D、F,若AD=18,则△ABC的周长为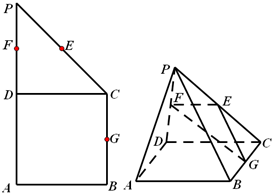 如图,在直角梯形ABCP中,BC∥AP,AB⊥BC,CD⊥AP,AD=CD=PD,E,F,G分别为线段PC,PD,BC的中点,现将△PDC折起,使点P∉平面ABCD.求证:PA∥面EFG.
如图,在直角梯形ABCP中,BC∥AP,AB⊥BC,CD⊥AP,AD=CD=PD,E,F,G分别为线段PC,PD,BC的中点,现将△PDC折起,使点P∉平面ABCD.求证:PA∥面EFG.