题目内容
17.设tanα=3,则$\frac{sin(α-π)+cos(π-α)}{sin(\frac{π}{2}-α)+cos(\frac{π}{2}+α)}$=2.分析 利用诱导公式、同角三角函数的基本关系化简所给的式子,可得结果.
解答 解:∵tanα=3,则$\frac{sin(α-π)+cos(π-α)}{sin(\frac{π}{2}-α)+cos(\frac{π}{2}+α)}$=$\frac{-sinα+(-cosα)}{cosα+(-sinα)}$=$\frac{sinα+cosα}{sinα-cosα}$
=$\frac{tanα+1}{tanα-1}$=$\frac{3+1}{3-1}$=2,
故答案为:2.
点评 本题主要考查同角三角函数的基本关系、诱导公式的应用,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
5.已知函数f(x)=alnx-$\frac{1}{2}{x^2}$+bx存在极小值,则有( )
| A. | a<0,b>0 | B. | a>0,b>0 | C. | a<0,b<0 | D. | a>0,b<0 |
6.已知变量x,y满足约束条件$\left\{\begin{array}{l}x-y≥2\\ x+y≤4\\ y≥-1\end{array}\right.$,则目标函数z=x-2y的最小值为( )
| A. | -1 | B. | 1 | C. | 3 | D. | 7 |
7.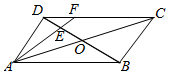 在平行四边形ABCD中,AC与BD交于点O,E是线段OD的中点,AE的延长线与CD相交于点F.若AB=2,$AD=\sqrt{2}$,∠BAD=45°,则$\overrightarrow{AF}•\overrightarrow{BE}$=( )
在平行四边形ABCD中,AC与BD交于点O,E是线段OD的中点,AE的延长线与CD相交于点F.若AB=2,$AD=\sqrt{2}$,∠BAD=45°,则$\overrightarrow{AF}•\overrightarrow{BE}$=( )
 在平行四边形ABCD中,AC与BD交于点O,E是线段OD的中点,AE的延长线与CD相交于点F.若AB=2,$AD=\sqrt{2}$,∠BAD=45°,则$\overrightarrow{AF}•\overrightarrow{BE}$=( )
在平行四边形ABCD中,AC与BD交于点O,E是线段OD的中点,AE的延长线与CD相交于点F.若AB=2,$AD=\sqrt{2}$,∠BAD=45°,则$\overrightarrow{AF}•\overrightarrow{BE}$=( )| A. | $\frac{1}{2}$ | B. | 1 | C. | -$\frac{1}{2}$ | D. | 1 |
 如图,已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的上顶点为A,左右顶点为B,C,右焦点为F,|AF|=3,且△ABC的周长为14.
如图,已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的上顶点为A,左右顶点为B,C,右焦点为F,|AF|=3,且△ABC的周长为14.