题目内容
2.已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$$+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),且椭圆上的点到一个焦点的最短距离为$\frac{\sqrt{3}}{3}$b.(Ⅰ)求椭圆C的离心率;
(Ⅱ)若点M($\sqrt{3}$,$\frac{\sqrt{3}}{2}$)在椭圆C上,直线l与椭圆C相交于A,B两点,与直线OM相交于点N,且N是线段AB的中点,求|AB|的最大值.
分析 (Ⅰ)由椭圆的性质可在:a-c=$\frac{\sqrt{3}}{3}$b,平方,利用椭圆的离心率公式,即可求得椭圆C的离心率;
(Ⅱ)将M代入椭圆方程,求得a和b的值,求得椭圆方程,利用韦达定理及中点坐标公式,代入求得k的值,利用弦长公式即可求得|AB|的最大值.
解答 解:(Ⅰ)由a-c=$\frac{\sqrt{3}}{3}$b,则(a-c)2=$\frac{1}{3}$b2,
由b2=a2-c2,整理得:2a2-3ac+a2=0,由e=$\frac{c}{a}$,
∴2e2-3e+1=0,
解得:e=1或e=$\frac{1}{2}$,
由0<e<1,
∴椭圆得离心率e=$\frac{1}{2}$,
(Ⅱ)由(Ⅰ)可知a=2c,则b2=3c2,
将M($\sqrt{3}$,$\frac{\sqrt{3}}{2}$)代入椭圆方程,则$\frac{{x}^{2}}{4{c}^{2}}+\frac{{y}^{2}}{3{c}^{2}}=1$,解得:c=1,
∴椭圆的方程为:$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1$,
直线OM的方程为y=$\frac{1}{2}$x,
当直线l的不存在时,AB的中点不在直线y=$\frac{1}{2}$x,故直线l的斜率存在,
设直线l的方程为y=kx+m,则$\left\{\begin{array}{l}{y=kx+m}\\{\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1}\end{array}\right.$,
整理得:(3+4m2)x2+8kmx+4m2-12=0,
则△=64k2m2-4(3+4m2)(4m2-12)=48(3+4k2-m2)>0,
设A(x1,y1),B(x2,y2),则x1+x2=-$\frac{8km}{3+4{k}^{2}}$,x1x2=$\frac{4{m}^{2}-12}{3+4{k}^{2}}$,
则y1+y2=k(x1+x2)+2m=$\frac{6m}{3+4{k}^{2}}$,
则AB的中点N(-$\frac{4km}{3+4{k}^{2}}$,$\frac{3m}{3+4{k}^{2}}$),
由N在直线y=$\frac{1}{2}$x,则-$\frac{4km}{3+4{k}^{2}}$=2×$\frac{3m}{3+4{k}^{2}}$,解得:k=-$\frac{3}{2}$,
则△=48(12-m2)>0,解得:-2$\sqrt{3}$<m<2$\sqrt{3}$,
则丨AB丨=$\sqrt{1+(\frac{3}{2})^{2}}$•$\sqrt{({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}}$=$\frac{\sqrt{13}}{2}$•$\sqrt{(\frac{12m}{3+9})^{2}-4×\frac{4{m}^{2}-12}{3+9}}$,
=$\frac{\sqrt{39}}{6}$•$\sqrt{12-{m}^{2}}$,
当m=0,则丨AB丨最大,且丨AB丨max=$\sqrt{13}$,
|AB|的最大值$\sqrt{13}$.
点评 本题考查椭圆的标准方程及简单几何性质,考查直线与椭圆的位置关系,考查韦达定理,弦长公式及中点坐标公式,考查计算能力,属于中档题.

 学业测评一课一测系列答案
学业测评一课一测系列答案| A. | (-∞,0)∪(2,+∞) | B. | (0,2] | C. | [0,2] | D. | Φ |
| A. | 10 | B. | -10 | C. | -20 | D. | -30 |
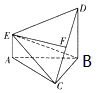 如图,在多面体ABCDE中,DB⊥平面ABC,AE⊥平面ABC,且△ABC是的边长为4的等边三角形,AE=2,CD与平面ABDE所成角的余弦值为$\frac{\sqrt{10}}{4}$,F是线段CD上一点.
如图,在多面体ABCDE中,DB⊥平面ABC,AE⊥平面ABC,且△ABC是的边长为4的等边三角形,AE=2,CD与平面ABDE所成角的余弦值为$\frac{\sqrt{10}}{4}$,F是线段CD上一点.