题目内容

7．函数f（x）的图象在点（2，f（2））处的切线方程为2x-y-3=0，则f（2）+f'（2）=3．

分析 先将x=2代入切线方程可求出f（2），再由切点处的导数为切线斜率可求出f'（2）的值，最后相加即可．

解答 解：根据题意，函数f（x）的图象在点（2，f（2））处的切线方程为2x-y-3=0，即y=2x-3，
则有f（2）=1，
又由切线的斜率k=2，则f'（2）=2；
则f（2）+f'（2）=1+2=3；
故答案为：3．

点评 本题主要考查导数的几何意义，即函数在某点的导数值等于以该点为切点的切线的斜率．

练习册系列答案
相关题目
17．将函数y=sinx+cosx图象上各点的横坐标缩短到原来的$\frac{1}{2}$倍，得到y=f（x）的图象，则y=f（x）的最小正周期为（　　）
A．$\frac{π}{2}$B．πC．2πD．4π
18．根据下列条件求抛物线方程：
（1）顶点在原点，焦点为F（0，$\frac{1}{4}$）的抛物线的标准方程；
（2）顶点在原点，准线方程为x=3的抛物线方程；
（3）顶点在原点，对称轴为坐标轴，焦点在直线y=2x-4上的抛物线方程．
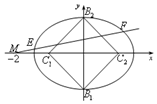15．已知椭圆C方程为$\frac{{x}^{2}}{{a}^{2}}$+y2=1，过右焦点斜率为l的直线到原点的距离为$\frac{\sqrt{2}}{2}$．
（Ⅰ）求椭圆C的方程；
（Ⅱ）设M（2，0），过点M的直线与椭圆C相交于E，F两点，当线段EF的中点落在由四点C1（-1，0），C2（1，0），B1（0，-1），B2（0，1）构成的四边形内（包括边界）时，求直线斜率的取值范围．
2．已知向量$\overrightarrow{a}$=（cos5°，sin5°），$\overrightarrow{b}$=（cos65°，sin65°），则|$\overrightarrow{a}$+2$\overrightarrow{b}$|=$\sqrt{7}$．
12．化简：$\frac{tan（2π-θ）sin（-2π-θ）cos（6π-θ）}{cos（θ-π）sin（5π+θ）}$．
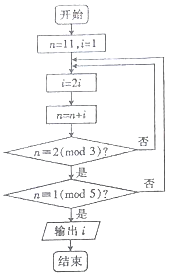19．若正整数N除以正整数m后的余数为n，则记为N=n（mod m），例如10=2（mod 4），下面程序框图的算法源于我国古代闻名中外的《中国剩余定理》．执行该程序框图，则输出的i等于（　　）
A．4B．8C．16D．32
16．已知函数f（x）=（mx-1）ex-x2．
（1）若曲线y=f（x）在点（1，f（1））处的切线斜率为e-2，求函数f（x）的单调区间；
（2）若关于x的不等式f（x）＜-x2+mx-m有且仅有两个整数解，求实数m的取值范围．
17．设tanα=3，则$\frac{sin（α-π）+cos（π-α）}{sin（\frac{π}{2}-α）+cos（\frac{π}{2}+α）}$=2．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网