题目内容
5.已知函数f(x)=alnx-$\frac{1}{2}{x^2}$+bx存在极小值,则有( )| A. | a<0,b>0 | B. | a>0,b>0 | C. | a<0,b<0 | D. | a>0,b<0 |
分析 求出函数的导数,利用极值点以及二次函数的性质,推出a,b符号,得到结果.
解答 解:函数f(x)=alnx-$\frac{1}{2}{x^2}$+bx定义域为:x>0,
可得函数f′(x)=$\frac{a}{x}$-x+b=$\frac{-{x}^{2}+bx+a}{x}$,
令-x2+bx+a=0,函数f(x)=alnx-$\frac{1}{2}{x^2}$+bx存在极小值,可得b2+4a>0,
∴极小值点x1=$\frac{b}{2}$-$\frac{\sqrt{{b}^{2}+4a}}{2}$>0,可得a<0,b>0.
故选:A.
点评 本题考查函数的极值点的判断与求法,注意函数的定义域,二次函数的性质的应用,考查转化思想以及计算能力.

练习册系列答案
相关题目
13.已知命题P:存在x∈R,mx2+1≤1,q对任意x∈R,x2+mx+1≥0,若p∨(¬q)为假命题,则实数m的取值范围是( )
| A. | (-∞,0)∪(2,+∞) | B. | (0,2] | C. | [0,2] | D. | Φ |
20.函数$f(x)=(sinx+\sqrt{3}cosx)(cosx-\sqrt{3}sinx)$的最小正周期是( )
| A. | $\frac{π}{2}$ | B. | π | C. | $\frac{3π}{2}$ | D. | 2π |
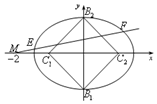 已知椭圆C方程为$\frac{{x}^{2}}{{a}^{2}}$+y2=1,过右焦点斜率为l的直线到原点的距离为$\frac{\sqrt{2}}{2}$.
已知椭圆C方程为$\frac{{x}^{2}}{{a}^{2}}$+y2=1,过右焦点斜率为l的直线到原点的距离为$\frac{\sqrt{2}}{2}$.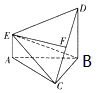 如图,在多面体ABCDE中,DB⊥平面ABC,AE⊥平面ABC,且△ABC是的边长为4的等边三角形,AE=2,CD与平面ABDE所成角的余弦值为$\frac{\sqrt{10}}{4}$,F是线段CD上一点.
如图,在多面体ABCDE中,DB⊥平面ABC,AE⊥平面ABC,且△ABC是的边长为4的等边三角形,AE=2,CD与平面ABDE所成角的余弦值为$\frac{\sqrt{10}}{4}$,F是线段CD上一点.