题目内容
9．已知等差数列{an}满足：a1+a5=4，则数列{2${\;}^{{a}_{n}}$}的前5项之积为1024（用数字作答）分析 根据等差数列的性质可得a1+a5=a2+a4=2a3=4，即可求出前5项和，再根据指数幂的运算性质即可求出答案．
解答 解：∵等差数列{an}满足：a1+a5=4，
∴a1+a5=a2+a4=2a3=4，
∴a1+a5+a2+a4+a3=4+4+2=10，
∴数列{2${\;}^{{a}_{n}}$}的前5项之积为2${\;}^{{a}_{1}+{a}_{2}+{a}_{3}+{a}_{4}+{a}_{5}}$=210=1024，
故答案为：1024
点评 本题考查了等差数列的性质和指数幂的运算性质，属于中档题
练习册系列答案
相关题目
19．
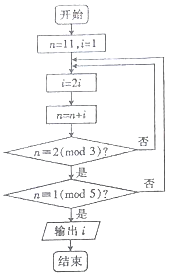若正整数N除以正整数m后的余数为n，则记为N=n（mod m），例如10=2（mod 4），下面程序框图的算法源于我国古代闻名中外的《中国剩余定理》．执行该程序框图，则输出的i等于（ ）
若正整数N除以正整数m后的余数为n，则记为N=n（mod m），例如10=2（mod 4），下面程序框图的算法源于我国古代闻名中外的《中国剩余定理》．执行该程序框图，则输出的i等于（ ）| A． | 4 | B． | 8 | C． | 16 | D． | 32 |
20．函数$f（x）=（sinx+\sqrt{3}cosx）（cosx-\sqrt{3}sinx）$的最小正周期是（ ）
| A． | $\frac{π}{2}$ | B． | π | C． | $\frac{3π}{2}$ | D． | 2π |
4．某校高三年级准备举行一次座谈会，其中三个班被邀请的学生数如表所示：
（Ⅰ）若从这10名学生中随机选出2名学生发言，求这2名学生不属于同一班级的概率；
（Ⅱ）若从这10名学生中随机选出3名学生发言，设X为来自高三（1）班的学生人数，求随机变量X的分布列和数学期望．
| 班级 | 高三（1） | 高三（2） | 高三（3） |
| 人数 | 3 | 3 | 4 |
（Ⅱ）若从这10名学生中随机选出3名学生发言，设X为来自高三（1）班的学生人数，求随机变量X的分布列和数学期望．
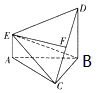如图，在多面体ABCDE中，DB⊥平面ABC，AE⊥平面ABC，且△ABC是的边长为4的等边三角形，AE=2，CD与平面ABDE所成角的余弦值为$\frac{\sqrt{10}}{4}$，F是线段CD上一点．
18．连续掷两次骰子，以先后得到的点数m，n为点P的坐标（m，n），那么点P在圆x2+y2=17内部（不包括边界）的概率是（ ）
| A． | $\frac{1}{4}$ | B． | $\frac{1}{6}$ | C． | $\frac{5}{18}$ | D． | $\frac{2}{9}$ |