题目内容
已知空间四边形OABC中,∠AOB=∠BOC=∠AOC,且OA=OB=OC,M、N分别是OA、BC的中点,G是MN的中点,求证:OG⊥BC.
考点:直线与平面垂直的性质
专题:空间向量及应用
分析:先画出图形,连接ON,设∠AOB=∠BOC=∠AOC=θ,
=
,
=
,
=
,则|
|=|
|=|
|,分别表示出
和
,通过计算
•
=0,从而证明OG⊥BC.
| OA |
| a |
| OB |
| b |
| OC |
| c |
| a |
| b |
| c |
| OG |
| BC |
| OG |
| BC |
解答:
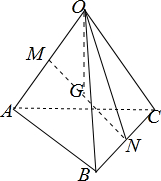 证明:如图示:
证明:如图示:
连接ON,设∠AOB=∠BOC=∠AOC=θ,
=
,
=
,
=
,
则|
|=|
|=|
|,
又
=
(
+
)
=
[
+
(
+
)]
=
(
+
+
),
=
-
,
∴
•
=
((
+
+
)•(
-
)
=
(|
|2cosθ-|
|2cosθ+|
|2-|
|2)
=0,
∴OG⊥BC.
 证明:如图示:
证明:如图示:连接ON,设∠AOB=∠BOC=∠AOC=θ,
| OA |
| a |
| OB |
| b |
| OC |
| c |
则|
| a |
| b |
| c |
又
| OG |
| 1 |
| 2 |
| OM |
| ON |
=
| 1 |
| 2 |
| 1 |
| 2 |
| OA |
| 1 |
| 2 |
| OB |
| OC |
=
| 1 |
| 4 |
| a |
| b |
| c |
| BC |
| c |
| b |
∴
| OG |
| BC |
| 1 |
| 4 |
| a |
| b |
| c |
| c |
| b |
=
| 1 |
| 4 |
| a |
| a |
| a |
| a |
=0,
∴OG⊥BC.
点评:本题考查了空间中直线和直线的位置关系,考查了向量的应用,是一道中档题.

练习册系列答案
相关题目
下列哪组中的函数f(x)与g(x)相等( )
A、f(x)=x2,g(x)=(
| ||||||
B、f(x)=x+1,g(x)=
| ||||||
C、f(x)=x,g(x)=
| ||||||
D、f(x)=
|
 在正方体ABCD-A1B1C1D1中,O为底面ABCD的中心,E、F分别为CC1、AD的中点,求异面直线OE与FD1所成角的余弦值.
在正方体ABCD-A1B1C1D1中,O为底面ABCD的中心,E、F分别为CC1、AD的中点,求异面直线OE与FD1所成角的余弦值.