题目内容
19.空气污染,又称为大气污染,当空气污染指数(单位:μg/m3)为0~50时,空气质量级别为一级,空气质量状况属于优;当空气污染指数为50~100时,空气质量级别为二级,空气质量状况属于良;当空气污染指数为
100~150时,空气质量级别为三级,空气质量状况属于轻度污染;当空气污染指数为150~200时,空气质量级别为四级,空气质量状况属于中度污染; 2015年1月某日某省x个监测0点数据统计如下:
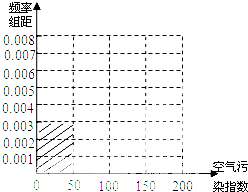
| 空气污染指数 (单位:μg/m3) | [0,50] | (50,100] | (100,150] | (150,200] |
| 监测点个数 | 15 | 40 | y | 15 |
(Ⅱ)统计部门从该省空气质量“良好”和“轻度污染”的两类监测点中采用分层抽样的方式抽取了7个监测点,省环保部门再从中随机选取3个监测点进行调研,记省环保部门“选到空气质量“良好”的城市个数为ξ”,求ξ的分布列.
分析 (Ⅰ)由题意得0.003×50=$\frac{15}{x}$,15+40+y+15=x,由此能求出x,y,进而能完成频率分布直方图.
(Ⅱ)空气良好有$\frac{7}{40+30}×40=4$个,轻度污染有$\frac{7}{40+30}×30=3$个,ξ的所有可能取值为0,1,2,3,分别求出相应的概率,由此能求出ξ的分布列.
解答 解:(Ⅰ)由题意得0.003×50=$\frac{15}{x}$,解得x=100,
又15+40+y+15=100,解得y=30.
∵$\frac{40}{100×50}$=0.008,$\frac{30}{100×50}=0.006$,$\frac{15}{100×50}=0.003$,
∴完成频率分布直方图,如下图:
(Ⅱ)空气良好有$\frac{7}{40+30}×40=4$个,轻度污染有$\frac{7}{40+30}×30=3$个,
ξ的所有可能取值为0,1,2,3,
P(ξ=0)=$\frac{{C}_{3}^{3}}{{C}_{7}^{3}}$=$\frac{1}{35}$,
P(ξ=1)=$\frac{{C}_{4}^{1}{C}_{3}^{2}}{{C}_{7}^{3}}$=$\frac{12}{35}$,
P(ξ=2)=$\frac{{C}_{4}^{2}{C}_{3}^{1}}{{C}_{7}^{3}}$=$\frac{18}{35}$,
P(ξ=3)=$\frac{{C}_{4}^{3}{C}_{3}^{0}}{{C}_{7}^{3}}$=$\frac{4}{35}$,
∴ξ的分布列为:
| ξ | 0 | 1 | 2 | 3 |
| P | $\frac{1}{35}$ | $\frac{12}{35}$ | $\frac{18}{35}$ | $\frac{4}{35}$ |
点评 本题考查频率分布直方图的应用,考查离散型随机变量的分布列的求法,是基础题,解题时要认真审题,注意排列组合知识的合理运用.

练习册系列答案
相关题目
8.已知tanα=2则cos($\frac{2015π}{2}$-2α)的值为( )
| A. | $\frac{4}{5}$ | B. | $-\frac{4}{5}$ | C. | 2 | D. | $-\frac{1}{2}$ |
9.cos(-$\frac{9π}{4}$)-sin(-$\frac{9π}{4}$)的值是( )
| A. | $\sqrt{2}$ | B. | -$\sqrt{2}$ | C. | 0 | D. | $\frac{\sqrt{2}}{2}$ |