题目内容
4.若正方体ABCD-A1B1C1D1中,E、F分别是D1C1、AB的中点,则A1B1与截面A1ECF所成的角的正切值为$\sqrt{2}$.分析 证明直线EF垂直平面A1B1C内的两条相交直线A1C、B1C,可得EF⊥平面A1B1C,从而B1在平面A1ECF上的射影在线段A1C上,则∠B1A1C就是A1B1与平面A1ECF所成的角.然后解三角形,求A1B1与平面A1ECF所成角的正切值,即可得出结论.
解答 解:连接C1B,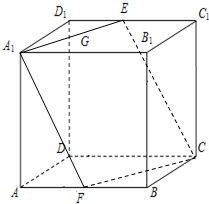
∵E、F分别为C1D1与AB的中点,
∴A1F=CE.
又A1F∥CE,
∴A1FCB为平行四边形,
∴C1B∥EF.
而C1B⊥B1C,
∴EF⊥B1C.
又四边形A1ECF是菱形,∴EF⊥A1C.∴EF⊥面A1B1C.
又EF?平面A1ECF,
∴平面A1B1C⊥平面A1ECF,
∴B1在平面A1ECF上的射影在线段A1C上.
∴∠B1A1C就是A1B1与平面A1ECF所成的角.
∵A1B1⊥B1C,在Rt△A1B1C中,tan∠B1A1C=$\sqrt{2}$.
∴A1B1与平面A1ECF所成角为arctan$\sqrt{2}$.
故答案为:$\sqrt{2}$.
点评 本题考查直线与平面垂直的判定,直线与平面所成的角,考查学生空间想象能力,逻辑思维能力,是中档题.

练习册系列答案
相关题目
5.已知函数$f(x)={x^2}+lg(x+\sqrt{{x^2}+1})$,若f(a)=M,则f(-a)等于( )
| A. | 2a2-M | B. | M-2a2 | C. | 2M-a2 | D. | a2-2M |
6.若a>b>0,0<c<1,则( )
| A. | logac<logbc | B. | ca>cb | C. | ac<ab | D. | logca<logcb |
12.点P所在轨迹的极坐标方程为ρ=2cosθ,点Q所在轨迹的参数方程为$\left\{\begin{array}{l}{x=1+t}\\{y=4+2t}\end{array}\right.$(t为参数),则|PQ|的最小值是( )
| A. | 2 | B. | $\frac{4\sqrt{5}}{5}$+1 | C. | 1 | D. | $\frac{4\sqrt{5}}{5}$-1 |
19.空气污染,又称为大气污染,当空气污染指数(单位:μg/m3)为0~50时,空气质量级别为一级,空气质量
状况属于优;当空气污染指数为50~100时,空气质量级别为二级,空气质量状况属于良;当空气污染指数为
100~150时,空气质量级别为三级,空气质量状况属于轻度污染;当空气污染指数为150~200时,空气质量级别为四级,空气质量状况属于中度污染; 2015年1月某日某省x个监测0点数据统计如下: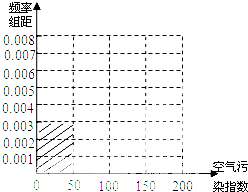
(Ⅰ)根据所给统计表和频率分布直方图中的信息求出x,y的值,并完成频率分布直方图;
(Ⅱ)统计部门从该省空气质量“良好”和“轻度污染”的两类监测点中采用分层抽样的方式抽取了7个监测点,省环保部门再从中随机选取3个监测点进行调研,记省环保部门“选到空气质量“良好”的城市个数为ξ”,求ξ的分布列.
状况属于优;当空气污染指数为50~100时,空气质量级别为二级,空气质量状况属于良;当空气污染指数为
100~150时,空气质量级别为三级,空气质量状况属于轻度污染;当空气污染指数为150~200时,空气质量级别为四级,空气质量状况属于中度污染; 2015年1月某日某省x个监测0点数据统计如下:

| 空气污染指数 (单位:μg/m3) | [0,50] | (50,100] | (100,150] | (150,200] |
| 监测点个数 | 15 | 40 | y | 15 |
(Ⅱ)统计部门从该省空气质量“良好”和“轻度污染”的两类监测点中采用分层抽样的方式抽取了7个监测点,省环保部门再从中随机选取3个监测点进行调研,记省环保部门“选到空气质量“良好”的城市个数为ξ”,求ξ的分布列.
16.若函数f(x)=x3-3x-a,当x∈[0,3]上时,m≤f(x)≤n恒成立,则n-m的最小值为( )
| A. | 2 | B. | 4 | C. | 18 | D. | 20 |