题目内容
1.已知函数f(x)=lnx+x2-1,g(x)=ex-e( I)试判断f(x)的单调性;
( II)若对于任意的x∈(1,+∞),mg(x)>f(x)恒成立,求实数m的取值范围.
分析 (Ⅰ)求导,根据导数和函数的单调性的关系即可判断,
(Ⅱ)由题意mg(x)>f(x)恒成立,得到m(ex-e)-lnx-x2+1>0,在(1,+∞)恒成立,令h(x)=m(ex-e)-lnx-x2+1,求导,再分类讨论,求出函数的最值,即可判断m的取值范围.
解答 解:(Ⅰ)∵f(x)=lnx+x2-1,x>0
∴f′(x)=$\frac{1}{x}$+2x>0恒成立,
∴f(x)在(0,+∞)为增函数,
(Ⅱ)∵mg(x)>f(x)恒成立,
∴m(ex-e)-lnx-x2+1>0,在(1,+∞)恒成立,
令h(x)=m(ex-e)-lnx-x2+1,
∴h′(x)=mex-$\frac{1}{x}$-2x,
令h′(1)=0
即me-3=0,可解得m=$\frac{3}{e}$.
①当m≤0时,显然h′(x)=mex-$\frac{1}{x}$-2x<0,
此时h(x)在(1,+∞)上单调递减,
∴h(x)<h(1)=0,不满足条件.
②当0<m<$\frac{3}{e}$时,令p(x)=mex-$\frac{1}{x}$,q(x)=2x.
显然p(x)=mex-$\frac{1}{x}$在[1,+∞)上单调递增,
∴p(x)min=p(1)=me-1<$\frac{3}{e}$×e-1=2
由q(x)=2x在[1,+∞)上单调递增,于是q(x)min=2.
∴p(x)min<q(x)min,
于是函数p(x)的图象与函数q(x)的图象只可能有两种情况:
若p(x)的图象恒在q(x)图象的下方,此时p(x)<h(x),即h′(x)<0,
故h(x)在(1,+∞)上单调递减,
又h(1)=0,故h(x)<0,不满足条件.
若p(x)的图象与q(x)的图象在x>1某点处的相交,设第一个交点的横坐标为x0,
当x∈(1,x0)时,p(x)<q(x),即h′(x)<0,故h(x)在(1,x0)上单调递减,
又h(1)=0,故当x∈(1,x0)时,h(x)<0.
∴h(x)不可能恒大于0,不满足条件.
③当m≥$\frac{3}{e}$时,令φ(x)=mex-$\frac{1}{x}$-2x,则φ′(x)=mex+$\frac{1}{{x}^{2}}$-2,
∵x∈(1,+∞),
∴φ′(x)=mex+$\frac{1}{{x}^{2}}$-2>mex-2≥$\frac{3}{e}$×e-2=1>0
故φ(x)=mex-$\frac{1}{x}$-2x在(1,+∞)上单调递增,
于是φ(x)>φ(1)=me-1-2>$\frac{3}{e}×e$-3=0
即h′(x)>0
∴h(x)在(1,+∞)上单调递增,
∴h(x)>h(1)=0成立.
综上,实数m的取值范围是m≥$\frac{e}{3}$)
点评 本题考查了导数和函数的单调性和最值得关系,以及不等式恒成立的问题,关键是构造函数,培养的学生应用能力,运算能力,转化能力,属于难题.

| A. | 1 | B. | $\frac{{\sqrt{7}}}{7}$ | C. | -1 | D. | $\frac{2\sqrt{7}}{7}$ |
| A. | -$\frac{14}{5}$ | B. | -$\frac{7}{5}$ | C. | -2 | D. | $\frac{4}{5}$ |
| A. | logac<logbc | B. | ca>cb | C. | ac<ab | D. | logca<logcb |
| A. | 5或6个 | B. | 3或9个 | C. | 9或10个 | D. | 5或9个 |
状况属于优;当空气污染指数为50~100时,空气质量级别为二级,空气质量状况属于良;当空气污染指数为
100~150时,空气质量级别为三级,空气质量状况属于轻度污染;当空气污染指数为150~200时,空气质量级别为四级,空气质量状况属于中度污染; 2015年1月某日某省x个监测0点数据统计如下:
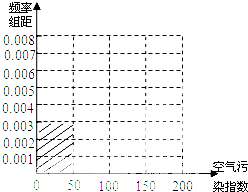
| 空气污染指数 (单位:μg/m3) | [0,50] | (50,100] | (100,150] | (150,200] |
| 监测点个数 | 15 | 40 | y | 15 |
(Ⅱ)统计部门从该省空气质量“良好”和“轻度污染”的两类监测点中采用分层抽样的方式抽取了7个监测点,省环保部门再从中随机选取3个监测点进行调研,记省环保部门“选到空气质量“良好”的城市个数为ξ”,求ξ的分布列.
| A. | {x=3或y=1} | B. | {3,1} | C. | {(3,1)} | D. | (3,1) |