题目内容
9．cos（-$\frac{9π}{4}$）-sin（-$\frac{9π}{4}$）的值是（ ）| A． | $\sqrt{2}$ | B． | -$\sqrt{2}$ | C． | 0 | D． | $\frac{\sqrt{2}}{2}$ |
分析 利用诱导公式化简即可．
解答 解：cos（-$\frac{9π}{4}$）-sin（-$\frac{9π}{4}$）=cos（$\frac{9π}{4}$）+sin（$\frac{9π}{4}$）=cos（2π+$\frac{π}{4}$）+sin（2π+$\frac{π}{4}$）=$\frac{\sqrt{2}}{2}+\frac{\sqrt{2}}{2}$=$\sqrt{2}$．
故选A．
点评 本题考查了诱导公式化简计算和特殊三角函数值．比较基础．
练习册系列答案
小学教材全测系列答案
小学数学口算题卡脱口而出系列答案
优秀生应用题卡口算天天练系列答案
浙江之星课时优化作业系列答案
相关题目
19．空气污染，又称为大气污染，当空气污染指数（单位：μg/m3）为0～50时，空气质量级别为一级，空气质量
状况属于优；当空气污染指数为50～100时，空气质量级别为二级，空气质量状况属于良；当空气污染指数为
100～150时，空气质量级别为三级，空气质量状况属于轻度污染；当空气污染指数为150～200时，空气质量级别为四级，空气质量状况属于中度污染； 2015年1月某日某省x个监测0点数据统计如下：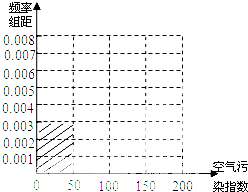
（Ⅰ）根据所给统计表和频率分布直方图中的信息求出x，y的值，并完成频率分布直方图；
（Ⅱ）统计部门从该省空气质量“良好”和“轻度污染”的两类监测点中采用分层抽样的方式抽取了7个监测点，省环保部门再从中随机选取3个监测点进行调研，记省环保部门“选到空气质量“良好”的城市个数为ξ”，求ξ的分布列．
状况属于优；当空气污染指数为50～100时，空气质量级别为二级，空气质量状况属于良；当空气污染指数为
100～150时，空气质量级别为三级，空气质量状况属于轻度污染；当空气污染指数为150～200时，空气质量级别为四级，空气质量状况属于中度污染； 2015年1月某日某省x个监测0点数据统计如下：
| 空气污染指数 （单位：μg/m3） | [0，50] | （50，100] | （100，150] | （150，200] |
| 监测点个数 | 15 | 40 | y | 15 |
（Ⅱ）统计部门从该省空气质量“良好”和“轻度污染”的两类监测点中采用分层抽样的方式抽取了7个监测点，省环保部门再从中随机选取3个监测点进行调研，记省环保部门“选到空气质量“良好”的城市个数为ξ”，求ξ的分布列．
20．设A={（x，y）|2x+y=7}，B={（x，y）|x+2y=5}，则A∩B=（ ）
| A． | {x=3或y=1} | B． | {3，1} | C． | {（3，1）} | D． | （3，1） |
17．设数列{an}的通项公式为an=2n-7（n∈N*）则|a1|+|a2|+…+|a7|=（ ）
| A． | 7 | B． | 0 | C． | 18 | D． | 25 |
4．设An和Bn是等差数列{an}和{bn}的前n项和，若$\frac{a_5}{b_7}=1$，则$\frac{A_9}{{{B_{13}}}}$=（ ）
| A． | $\frac{9}{13}$ | B． | $\frac{5}{7}$ | C． | $\frac{17}{25}$ | D． | 1 |
1．函数y=$\frac{1}{2}{x}^{2}-lnx$的单调减区间是（ ）
| A． | （0，1） | B． | （0，1）∪（-∞，-1） | C． | （-∞，1） | D． | （-∞，+∞） |
19．某班主任对全班50名学生进行了作业量多少的调查，根据列联表数据计算得到K2=5.059，因为P（K2≥5.024）=0.025，则认为“喜欢玩电脑游戏与认为作业量的多少有关系”的把握大约为（ ）
| A． | 2.5% | B． | 95% | C． | 97.5% | D． | 不具有相关性 |