题目内容
11.函数y=x2•(1-3x)在(0,$\frac{1}{3}$)上的最大值是$\frac{1}{12}$.分析 由于0<x<$\frac{1}{3}$,可得1-3x>0,变形利用基本不等式可得y=x2(1-3x)即可得出.
解答 解:∵0<x<$\frac{1}{3}$,∴1-3x>0,
∴函数y=x2(1-3x)=$\frac{2}{3}$$•x•x•(\frac{3}{2}-2x)$≤$\frac{2}{3}$•$(\frac{\frac{3}{2}+x+x-2x}{3})^{3}$=$\frac{1}{12}$,当且仅当x=$\frac{1}{2}$时取等号.
故答案为:$\frac{1}{12}$.
点评 本题考查了变形利用基本不等式,考查转化思想的应用,属于基础题.也可以利用导数求解函数的最值.

练习册系列答案
相关题目
2.已知函数f(x)=x3-3x,则函数h(x)=f[f(x)]-c,c∈[-2,2]的零点个数( )
| A. | 5或6个 | B. | 3或9个 | C. | 9或10个 | D. | 5或9个 |
19.空气污染,又称为大气污染,当空气污染指数(单位:μg/m3)为0~50时,空气质量级别为一级,空气质量
状况属于优;当空气污染指数为50~100时,空气质量级别为二级,空气质量状况属于良;当空气污染指数为
100~150时,空气质量级别为三级,空气质量状况属于轻度污染;当空气污染指数为150~200时,空气质量级别为四级,空气质量状况属于中度污染; 2015年1月某日某省x个监测0点数据统计如下: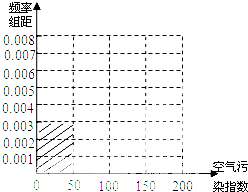
(Ⅰ)根据所给统计表和频率分布直方图中的信息求出x,y的值,并完成频率分布直方图;
(Ⅱ)统计部门从该省空气质量“良好”和“轻度污染”的两类监测点中采用分层抽样的方式抽取了7个监测点,省环保部门再从中随机选取3个监测点进行调研,记省环保部门“选到空气质量“良好”的城市个数为ξ”,求ξ的分布列.
状况属于优;当空气污染指数为50~100时,空气质量级别为二级,空气质量状况属于良;当空气污染指数为
100~150时,空气质量级别为三级,空气质量状况属于轻度污染;当空气污染指数为150~200时,空气质量级别为四级,空气质量状况属于中度污染; 2015年1月某日某省x个监测0点数据统计如下:

| 空气污染指数 (单位:μg/m3) | [0,50] | (50,100] | (100,150] | (150,200] |
| 监测点个数 | 15 | 40 | y | 15 |
(Ⅱ)统计部门从该省空气质量“良好”和“轻度污染”的两类监测点中采用分层抽样的方式抽取了7个监测点,省环保部门再从中随机选取3个监测点进行调研,记省环保部门“选到空气质量“良好”的城市个数为ξ”,求ξ的分布列.
16.若函数f(x)=x3-3x-a,当x∈[0,3]上时,m≤f(x)≤n恒成立,则n-m的最小值为( )
| A. | 2 | B. | 4 | C. | 18 | D. | 20 |
20.设A={(x,y)|2x+y=7},B={(x,y)|x+2y=5},则A∩B=( )
| A. | {x=3或y=1} | B. | {3,1} | C. | {(3,1)} | D. | (3,1) |
1.函数y=$\frac{1}{2}{x}^{2}-lnx$的单调减区间是( )
| A. | (0,1) | B. | (0,1)∪(-∞,-1) | C. | (-∞,1) | D. | (-∞,+∞) |