题目内容
13.已知函数f(x)=3sin(3x+φ),x∈[0,π],则y=f(x)的图象与直线y=2的交点个数最多有( )| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
分析 令f(x)=2,得sin(3x+φ)=$\frac{2}{3}$,根据x∈[0,π],求出3x+φ的取值范围,根据正弦函数的图象与性质,可得出函数y=f(x)的图象与直线y=2的交点最多有4个.
解答 解:令f(x)=3sin(3x+φ)=2,
得sin(3x+φ)=$\frac{2}{3}$∈(-1,1),
又x∈[0,π],∴3x∈[0,3π],
∴3x+φ∈[φ,3π+φ];
根据正弦函数的图象与性质,可得
该方程在正弦函数一个半周期上最多有4个解,
即函数y=f(x)的图象与直线y=2的交点最多有4个.
故选:C.
点评 本题主要考查了函数图象交点个数的判断问题,利用函数和方程之间的关系,进行求解即可.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
3.已知偶函数f(x)的定义域为R,且在(-∞,0)上是增函数,则f(-$\frac{3}{4}$)与f(a2-a+1)的大小关系为( )
| A. | f(-$\frac{3}{4}$)<f(a2-a+1) | B. | f(-$\frac{3}{4}$)>f(a2-a+1) | C. | f(-$\frac{3}{4}$)≤f(a2-a+1) | D. | f(-$\frac{3}{4}$)≥f(a2-a+1) |
8.已知a为实数,设函数f(x)=$\left\{\begin{array}{l}{x-{2}^{a},x<2}\\{lo{g}_{2}(x-2),x≥2}\end{array}\right.$,则f(2a+2)的值为( )
| A. | 2a | B. | a | C. | 2 | D. | a或2 |
5.函数f(x+1)是偶函数,则函数y=f(x)的图象关于( )
| A. | 直线x=1对称 | B. | 直线x=-1对称 | C. | 点(1,0)对称 | D. | 点(-1,0)对称 |
2.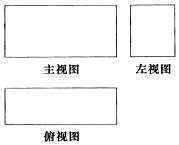 某长方体的三视图如图,长度为$\sqrt{10}$的体对角线在主视图中的投影长度为$\sqrt{6}$,在左视图中的投影长度为$\sqrt{5}$,则该长方体的体积为( )
某长方体的三视图如图,长度为$\sqrt{10}$的体对角线在主视图中的投影长度为$\sqrt{6}$,在左视图中的投影长度为$\sqrt{5}$,则该长方体的体积为( )
 某长方体的三视图如图,长度为$\sqrt{10}$的体对角线在主视图中的投影长度为$\sqrt{6}$,在左视图中的投影长度为$\sqrt{5}$,则该长方体的体积为( )
某长方体的三视图如图,长度为$\sqrt{10}$的体对角线在主视图中的投影长度为$\sqrt{6}$,在左视图中的投影长度为$\sqrt{5}$,则该长方体的体积为( )| A. | 3$\sqrt{5}$+2 | B. | 2$\sqrt{5}$ | C. | 6$\sqrt{5}$+4 | D. | 10 |