题目内容
18.已知a>0,b>0,且满足3a+b=a2+ab,则2a+b的最小值为3+2$\sqrt{2}$.分析 由a>0,b>0,且满足3a+b=a2+ab,可得b=$\frac{{a}^{2}-3a}{1-a}$>0,解得1<a<3.则2a+b=2a+$\frac{{a}^{2}-3a}{1-a}$=a-1+$\frac{2}{a-1}$+3,利用基本不等式的性质即可得出.
解答 解:由a>0,b>0,且满足3a+b=a2+ab,∴b=$\frac{{a}^{2}-3a}{1-a}$>0,解得1<a<3.
则2a+b=2a+$\frac{{a}^{2}-3a}{1-a}$=a-1+$\frac{2}{a-1}$+3≥2$\sqrt{(a-1)•\frac{2}{a-1}}$+3=2$\sqrt{2}$+3,当且仅当a=1+$\sqrt{2}$,b=1时取等号.
故答案为:3+2$\sqrt{2}$.
点评 本题考查了基本不等式的性质,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
6.设复数z=1-i(i是虚数单位),则$\frac{2}{z}$+z等于( )
| A. | 2 | B. | -2 | C. | 2i | D. | -2i |
13.已知函数f(x)=3sin(3x+φ),x∈[0,π],则y=f(x)的图象与直线y=2的交点个数最多有( )
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
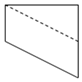
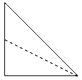
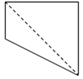
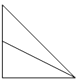
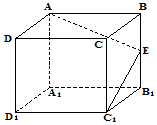 如图,正方体ABCD-A1B1C1D1中,E为棱BB1的中点,用过点A、E、C1的平面截去该正方体的下半部分,则剩余几何体的正视图(也称主视图)是( )
如图,正方体ABCD-A1B1C1D1中,E为棱BB1的中点,用过点A、E、C1的平面截去该正方体的下半部分,则剩余几何体的正视图(也称主视图)是( )