题目内容
已知点A(4,-3)和B(2,-1),点P满足|PA|=|PB|,则点P的轨迹方程是 .
考点:直线的一般式方程与直线的垂直关系
专题:直线与圆
分析:由中点坐标公式求出AB的中点坐标,由两点求斜率得到AB所在直线的斜率,求其负倒数得AB的垂直平分线的斜率,然后由直线方程的点斜式得点P的轨迹方程.
解答:
解:由点P满足|PA|=|PB|,可知点P的轨迹为点A(4,-3)和B(2,-1)的垂直平分线.
∵A(4,-3),B(2,-1),
由中点坐标公式得AB的中点为(
,
)=(3,-2),
kAB=
=-1,
∴其垂直平分线的斜率为1.
∴点P的轨迹方程是y+2=x-3,
即x-y-5=0.
故答案为:x-y-5=0.
∵A(4,-3),B(2,-1),
由中点坐标公式得AB的中点为(
| 4+2 |
| 2 |
| -3-1 |
| 2 |
kAB=
| -3-(-1) |
| 4-2 |
∴其垂直平分线的斜率为1.
∴点P的轨迹方程是y+2=x-3,
即x-y-5=0.
故答案为:x-y-5=0.
点评:本题考查了中点坐标公式,考查了直线的垂直与斜率之间的关系,是基础的计算题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
以下程序运行后的输出结果为( )


| A、21 | B、13 | C、17 | D、25 |
下列说法正确的是( )
| A、对立事件也是互斥事件 |
| B、某事件发生的概率为1.1 |
| C、不能同时发生的两个事件是两个对立事件 |
| D、某事件发生的概率是随着实验次数的变化而变化的 |
下列各数中,最大的是( )
| A、32(8) |
| B、111(5) |
| C、101010(2) |
| D、54(6) |
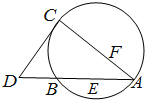 如图,CD为△ABC外接圆的切线,AB的延长线交直线CD于点D,E,F分别为弦AB与弦AC上的点,且BC•AE=DC•AF,B,E,F,C四点共圆.若DB=BE=EA,则过B,E,F,C四点的圆的面积与△ABC外接圆面积的比值为
如图,CD为△ABC外接圆的切线,AB的延长线交直线CD于点D,E,F分别为弦AB与弦AC上的点,且BC•AE=DC•AF,B,E,F,C四点共圆.若DB=BE=EA,则过B,E,F,C四点的圆的面积与△ABC外接圆面积的比值为