题目内容
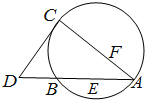 如图,CD为△ABC外接圆的切线,AB的延长线交直线CD于点D,E,F分别为弦AB与弦AC上的点,且BC•AE=DC•AF,B,E,F,C四点共圆.若DB=BE=EA,则过B,E,F,C四点的圆的面积与△ABC外接圆面积的比值为
如图,CD为△ABC外接圆的切线,AB的延长线交直线CD于点D,E,F分别为弦AB与弦AC上的点,且BC•AE=DC•AF,B,E,F,C四点共圆.若DB=BE=EA,则过B,E,F,C四点的圆的面积与△ABC外接圆面积的比值为考点:圆的切线的性质定理的证明
专题:立体几何
分析:如图所示.连接BC,EF.由于DC是△ABC的外接圆的切线,可得∠DCB=∠EAF.已知BC•AE=DC•AF,可得
=
.进而得到△BCD≌△FAE.于是∠CBD=∠AFE.由于E,F,C四点共圆.可得∠AFE=∠CBE.
于是∠CBD=∠CBE.进而得到∠CBE=90°.AC是△ABC的外接圆的直径,CE是E,F,C四点所在圆的直径.
不妨设DB=1.则BE=EA=DB=1.利用切割线定理可得:DC2=DB•DA.在△DCE中,由DB=BE,CB⊥DE.可得CE=DC.
在Rt△CBE中,CB2=CE2-BE2.在Rt△ABC中,AC2=BC2+AB2.可得:过B,E,F,C四点的圆的面积与△ABC外接圆面积的比值=
=
即可得出.
| BC |
| AF |
| DC |
| AE |
于是∠CBD=∠CBE.进而得到∠CBE=90°.AC是△ABC的外接圆的直径,CE是E,F,C四点所在圆的直径.
不妨设DB=1.则BE=EA=DB=1.利用切割线定理可得:DC2=DB•DA.在△DCE中,由DB=BE,CB⊥DE.可得CE=DC.
在Rt△CBE中,CB2=CE2-BE2.在Rt△ABC中,AC2=BC2+AB2.可得:过B,E,F,C四点的圆的面积与△ABC外接圆面积的比值=
π(
| ||
π(
|
| CE2 |
| AC2 |
解答:
解:如图所示.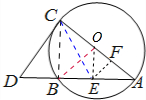
连接BC,EF.∵DC是△ABC的外接圆的切线,∴∠DCB=∠EAF.
∵BC•AE=DC•AF,∴
=
.
∴△BCD≌△FAE.
∴∠CBD=∠AFE.
∵E,F,C四点共圆.
∴∠AFE=∠CBE.
∴∠CBD=∠CBE.
又∵∠CBD+∠CBE=180°,∴∠CBE=90°.
∴AC是△ABC的外接圆的直径,CE是E,F,C四点所在圆的直径.
不妨设DB=1.则BE=EA=DB=1.
由切割线定理可得:DC2=DB•DA=1×3,DC=
.
在△DCE中,由DB=BE,CB⊥DE.∴CE=DC=
.
在Rt△CBE中,CB2=CE2-BE2=(
)2-12=2.
在Rt△ABC中,AC2=BC2+AB2=2+22=6.
∴过B,E,F,C四点的圆的面积与△ABC外接圆面积的比值=
=
=
=
.
故答案为:
.

连接BC,EF.∵DC是△ABC的外接圆的切线,∴∠DCB=∠EAF.
∵BC•AE=DC•AF,∴
| BC |
| AF |
| DC |
| AE |
∴△BCD≌△FAE.
∴∠CBD=∠AFE.
∵E,F,C四点共圆.
∴∠AFE=∠CBE.
∴∠CBD=∠CBE.
又∵∠CBD+∠CBE=180°,∴∠CBE=90°.
∴AC是△ABC的外接圆的直径,CE是E,F,C四点所在圆的直径.
不妨设DB=1.则BE=EA=DB=1.
由切割线定理可得:DC2=DB•DA=1×3,DC=
| 3 |
在△DCE中,由DB=BE,CB⊥DE.∴CE=DC=
| 3 |
在Rt△CBE中,CB2=CE2-BE2=(
| 3 |
在Rt△ABC中,AC2=BC2+AB2=2+22=6.
∴过B,E,F,C四点的圆的面积与△ABC外接圆面积的比值=
π(
| ||
π(
|
| CE2 |
| AC2 |
| 3 |
| 6 |
| 1 |
| 2 |
故答案为:
| 1 |
| 2 |
点评:本题综合考查了圆的性质、切割线定理、四点共圆的性质、相似三角形的性质、等腰三角形的性质、勾股定理、圆的面积之比等基础知识与基本技能方法,考查了推理能力和计算能力,属于难题.

练习册系列答案
相关题目
若α=
,则计算1+sin(α-2π)•sin(π+α)-2cos2(-α)所得的结果为( )
| 7π |
| 6 |
A、-
| ||
B、-
| ||
| C、0 | ||
D、
|
