题目内容
已知f（x）=2sin（2x+
）．则f（
）= ；若f（x）=-2，则满足条件的x的集合为 ；则f（x）的其中一个对称中心为 ．
| π |
| 3 |
| π |
| 6 |
考点：正弦函数的图象
专题：三角函数的求值,三角函数的图像与性质
分析：①直接利用函数的解析式求出函数的值
②利用整体思想求出函数的对称轴，进一步求出x所满足的集合．
③利用整体思想求出函数的对称中心．
②利用整体思想求出函数的对称轴，进一步求出x所满足的集合．
③利用整体思想求出函数的对称中心．
解答：
解：①已知已知f（x）=2sin（2x+
）．
则：f（
）=2sin
=
②若f（x）=-2，
则：sin（2x+
）=-1
则：2x+
=2kπ-
（k∈Z）
解得：x=kπ-
（k∈Z）
③令2x+
=kπ
解得：x=
-
（k∈Z）
| π |
| 3 |
则：f（
| π |
| 6 |
| 2π |
| 3 |
| 3 |
②若f（x）=-2，
则：sin（2x+
| π |
| 3 |
则：2x+
| π |
| 3 |
| π |
| 2 |
解得：x=kπ-
| 5π |
| 12 |
③令2x+
| π |
| 3 |
解得：x=
| kπ |
| 2 |
| π |
| 6 |
点评：本题考查的知识要点：三角函数的求值，正弦型函数的对称轴和对称中心的应用，属于基础题型．
练习册系列答案
新课标阶梯阅读训练系列答案
口算心算速算应用题系列答案
相关题目
已知一个几何体的三视图是三个全等的边长为l的正方形，如图所示，则该几何体的体积为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
函数f（x）=3cos2
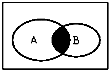已知全集U为实数集，集合 A={x|x2-2x-3＜0}，B={x|y=ln（1-x）}，则如图中阴影部分表示的集合为（ ）| A、{x|x-1≤x＜3} |
| B、{x|x＜3} |
| C、{x|x≤-1} |
| D、{x|-1＜x＜1} |