题目内容
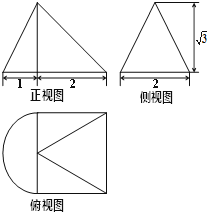
多面体的三视图如图所示，则该多面体体积为（单位cm） ．
考点：由三视图求面积、体积
专题：空间位置关系与距离
分析：如图所示，由三视图可知：该几何体为三棱锥P-ABC．该几何体可以看成是两个底面均为△PCD，高分别为AD和BD的棱锥形成的组合体，进而可得答案．
解答：
解：如图所示，
由三视图可知：
该几何体为三棱锥P-ABC．
该几何体可以看成是两个底面均为△PCD，高分别为AD和BD的棱锥形成的组合体，
由几何体的俯视图可得：△PCD的面积S=
×4×4=8cm2，
由几何体的正视图可得：AD+BD=AB=4cm，
故几何体的体积V=
×8×4=
cm3，
故答案为：
cm3
由三视图可知：
该几何体为三棱锥P-ABC．
该几何体可以看成是两个底面均为△PCD，高分别为AD和BD的棱锥形成的组合体，
由几何体的俯视图可得：△PCD的面积S=
| 1 |
| 2 |
由几何体的正视图可得：AD+BD=AB=4cm，
故几何体的体积V=
| 1 |
| 3 |
| 32 |
| 3 |
故答案为：
| 32 |
| 3 |
点评：本题考查由三视图求几何体的体积和表面积，根据已知的三视图分析出几何体的形状是关键．
练习册系列答案
相关题目
若曲线C1：y=ax2（a＞0）与曲线C2：y=ex存在公共切线，则a的取值范围为（ ）
A、[
| ||
B、(0，
| ||
C、[
| ||
D、(0，
|
阅读如图的程序框图，输出的值为（ ）
A、-
| ||
B、
| ||
| C、-1 | ||
D、-
|
