题目内容
在(2
-
)9的展开式中,各项系数之和为 .
| x |
| 1 |
| x |
考点:二项式系数的性质
专题:二项式定理
分析:在(2
-
)9的展开式中,令x=1,可得各项系数之和.
| x |
| 1 |
| x |
解答:
解:在(2
-
)9的展开式中,令x=1,可得各项系数之和为 19=1,
故答案为:1.
| x |
| 1 |
| x |
故答案为:1.
点评:本题主要考查二项式定理的应用,是给变量赋值的问题,关键是根据要求的结果,选择合适的数值代入,属于基础题.

练习册系列答案
相关题目
阅读如图的程序框图,输出的值为( )


A、-
| ||
B、
| ||
| C、-1 | ||
D、-
|
已知数列{an}为等比数列,a5=1,a9=81,则a7=( )
| A、9或-9 | B、9 |
| C、27或-27 | D、-27 |
已知全集U=(-1,1),集合A={1,2},B={2,3,4},则(∁UA)∩B=( )
| A、{2} |
| B、{3,4} |
| C、{1,4,5} |
| D、{2,3,4,5} |
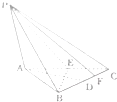 在三棱锥P-ABC中,底面ABC是边长为2的正三角形,PA⊥平面ABC,D,E分别为BC,AC的中点,F是CD的中点.
在三棱锥P-ABC中,底面ABC是边长为2的正三角形,PA⊥平面ABC,D,E分别为BC,AC的中点,F是CD的中点.