题目内容
对于函数f1(x),f2(x),h(x),如果存在实数a,b使得h(x)=a•f1(x)+b•f2(x),那么称h(x)为f1(x),f2(x)的生成函数.
(Ⅰ)下面给出两组函数,h(x)是否分别为f1(x),f2(x)的生成函数?并说明理由;
第一组:f1(x)=sinx,f2(x)=cosx,h(x)=sin(x+
);
第二组:f1(x)=x2-x,f2(x)=x2+x+1,h(x)=x2-x+1;
(Ⅱ)设f1(x)=log2x,f2(x)=log
x,a=2,b=1,生成函数h(x).若不等式3h2(x)+2h(x)+t<0在x∈[2,4]上有解,求实数t的取值范围.
(Ⅰ)下面给出两组函数,h(x)是否分别为f1(x),f2(x)的生成函数?并说明理由;
第一组:f1(x)=sinx,f2(x)=cosx,h(x)=sin(x+
| π |
| 3 |
第二组:f1(x)=x2-x,f2(x)=x2+x+1,h(x)=x2-x+1;
(Ⅱ)设f1(x)=log2x,f2(x)=log
| 1 |
| 2 |
考点:抽象函数及其应用
专题:函数的性质及应用
分析:(Ⅰ)根据生成函数的定义进行判断,看是否存在适合条件的a,b的值;
(Ⅱ)先化简得到h(x)=log2x,由x∈[2,4]知s=log2x∈[1,2],从而得到t<-3h2(x)-2h(x)=-3lo
x-2log2x的最大值-5.
(Ⅱ)先化简得到h(x)=log2x,由x∈[2,4]知s=log2x∈[1,2],从而得到t<-3h2(x)-2h(x)=-3lo
| g | 2 2 |
解答:
解:(Ⅰ)①设asinx+bcosx=sin(x+
),即asinx+bcosx=
sinx+
cosx,
取a=
, b=
,所以h(x)是f1(x),f2(x)的生成函数.
②设a(x2-x)+b(x2+x+1)=x2-x+1,即(a+b)x2-(a-b)x+b=x2-x+1,
则
,该方程组无解.所以h(x)不是f1(x),f2(x)的生成函数.
(Ⅱ)h(x)=2f1(x)+f2(x)=2log2x+log
x=log2x,
若不等式3h2(x)+2h(x)+t<0在x∈[2,4]上有解,
即当x∈[2,4]时有t<-3h2(x)-2h(x)=-3lo
x-2log2x
设s=log2x,则由x∈[2,4]知s∈[1,2],
令y=-3lo
x-2log2x=-3s2-2s=-3(s+
)2+
,
则ymax=-5,故t<-5.
| π |
| 3 |
| 1 |
| 2 |
| ||
| 2 |
取a=
| 1 |
| 2 |
| ||
| 2 |
②设a(x2-x)+b(x2+x+1)=x2-x+1,即(a+b)x2-(a-b)x+b=x2-x+1,
则
|
(Ⅱ)h(x)=2f1(x)+f2(x)=2log2x+log
| 1 |
| 2 |
若不等式3h2(x)+2h(x)+t<0在x∈[2,4]上有解,
即当x∈[2,4]时有t<-3h2(x)-2h(x)=-3lo
| g | 2 2 |
设s=log2x,则由x∈[2,4]知s∈[1,2],
令y=-3lo
| g | 2 2 |
| 1 |
| 3 |
| 1 |
| 3 |
则ymax=-5,故t<-5.
点评:本题考查了抽象函数的概念以及二次函数在给定区间上的最值问题,属于中档题.

练习册系列答案
 导学与测试系列答案
导学与测试系列答案 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目
设
•
=4,若
在
方向上的投影为
,且
在
方向上的投影为3,则
和
的夹角等于( )
| a |
| b |
| a |
| b |
| 2 |
| 3 |
| b |
| a |
| a |
| b |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
空间四边形OABC中,OB=OC,∠AOB=∠AOC=60°,则cos<
,
>=( )
| OA |
| BC |
A、
| ||||
B、
| ||||
C、-
| ||||
| D、0 |
在△ABC中,点G为△ABC的重心.已知|AB|=2
,且向量
与
的夹角为120°,则
•
的最小值是
( )
| 3 |
| GA |
| GB |
| CA |
| CB |
( )
| A、-3 | B、6 | C、9 | D、24 |
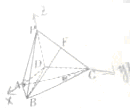 如图,在四棱锥P-ABCD中,底面ABCD是以AC为直径的圆的内接四边形,AC⊥BD,F是PC的中点,∠BAC=60°,PD⊥平面ABC.
如图,在四棱锥P-ABCD中,底面ABCD是以AC为直径的圆的内接四边形,AC⊥BD,F是PC的中点,∠BAC=60°,PD⊥平面ABC.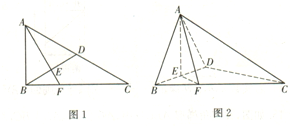
 工厂对一批产品进行抽样检测,如图是根据抽样检测后的产品重量(单位:克)数据绘制的频率分布直方图,其中产品重量的范围是[46,56],样本数据分组诶[46,48),[48,50),[50,52),[52,54),[54,56].若样本中产品重量小于50克的个数是36,则样本中重量不小于48克,并且小于54克的产品的个数是
工厂对一批产品进行抽样检测,如图是根据抽样检测后的产品重量(单位:克)数据绘制的频率分布直方图,其中产品重量的范围是[46,56],样本数据分组诶[46,48),[48,50),[50,52),[52,54),[54,56].若样本中产品重量小于50克的个数是36,则样本中重量不小于48克,并且小于54克的产品的个数是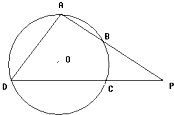 (选修4-1:几何证明选讲)如图,AB为⊙O的直径,过点B作⊙O的切线BC,OC交⊙O于点E,AE的延长线交BC于点D.若AB=BC=2,则CD=
(选修4-1:几何证明选讲)如图,AB为⊙O的直径,过点B作⊙O的切线BC,OC交⊙O于点E,AE的延长线交BC于点D.若AB=BC=2,则CD=