题目内容
4．如图，网格纸上小正方形的边长为1，粗实线画出的是某三棱锥的三视图，则该三棱锥的体积为（ ）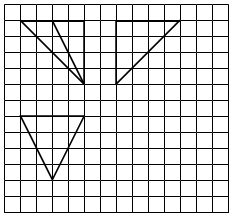
| A． | $\frac{16}{3}$ | B． | $\frac{{16\sqrt{3}}}{3}$ | C． | $\frac{32}{3}$ | D． | $\frac{64}{3}$ |
分析 根据三视图作出三棱锥的直观图，根据三视图中的数据计算棱锥的体积．
解答 
解由三视图可知三棱锥是从边长为4的正方体中截出来的M-ADD′，其中M为BC的中点．
∴三棱锥的体积V=$\frac{1}{3}{S}_{△ADM}•DD′$=$\frac{1}{3}×\frac{1}{2}×{4}^{2}×4$=$\frac{32}{3}$．
故选：C．
点评 本题考查了正方体的结构特征，棱锥的三视图和体积计算，属于基础题．
练习册系列答案
口算小状元口算速算天天练系列答案
天天练口算系列答案
相关题目
12．己知x，y满足约束条件$\left\{\begin{array}{l}{x-y-1≤0}\\{2x-y-3≥0}\end{array}\right.$，当目标函数z=ax+by（a＞0，b＞0）在该约束条件下取到最小值2$\sqrt{5}$时，则4a2+b2的最小值为（ ）
| A． | 5 | B． | 10 | C． | $\sqrt{5}$ | D． | $\sqrt{10}$ |
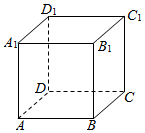如图，正方体ABCD-A1B1C1D1的棱长为1，请在此正方体中取出四个顶点构成一个三棱锥，满足三棱锥的四个面都是直角三角形，并求此三棱锥的体积．
16．在△ABC中，a=4，b=$\frac{5}{2}$，5cos（B+C）+3=0，则角B的大小为（ ）
| A． | $\frac{π}{6}$ | B． | $\frac{π}{4}$ | C． | $\frac{π}{3}$ | D． | $\frac{π}{6}$或$\frac{5π}{6}$ |