题目内容
19．化简$\sqrt{1-2tan{4cos}^{2}4}$+$\sqrt{1{-sin}^{2}4}$=-sin4．分析 根据同角三角函数的关系和三角函数的符号化简．
解答 解：∵57°＜1rad＜60°，∴228°＜4rad＜240°，
∴sin4＜cos4＜0，
∴$\sqrt{1-2tan{4cos}^{2}4}$+$\sqrt{1{-sin}^{2}4}$=$\sqrt{1-2sin4cos4}$+|cos4|=$\sqrt{（sin4-cos4）^{2}}$+|cos4|=cos4-sin4-cos4=-sin4．
故答案为：-sin4．
点评 本题考查了三角函数的化简，三角函数的性质，属于中档题．
练习册系列答案
文敬图书课时先锋系列答案
相关题目
4．如图，网格纸上小正方形的边长为1，粗实线画出的是某三棱锥的三视图，则该三棱锥的体积为（ ）
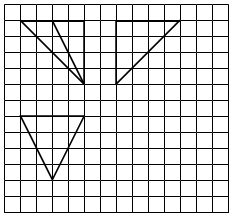
| A． | $\frac{16}{3}$ | B． | $\frac{{16\sqrt{3}}}{3}$ | C． | $\frac{32}{3}$ | D． | $\frac{64}{3}$ |
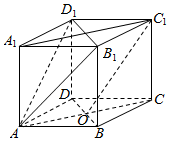在直平行六面体ABCD-A1B1C1D1中，底面ABCD是菱形，∠DAB=60°，AC∩BD=O，AB=AA1=1．
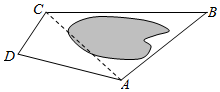如图，为了测量A，C两点间的距离，选取同一平面上B、D两点，测出四边形ABCD各边的长度（单位：km）：AB=5，BC=8，CD=3，DA=5，且∠B与∠D互补，则AC的长为7km．