题目内容
13.本着健康、低碳的生活理念,湛江市区采用公共自行车的人越来越多,使用年租卡租车的收费标准是每车每次不超过两小时免费,超过两小时的部分每小时收费2元(不足1小时的部分按1小时计算).假设甲、乙两人相互独立地用年租卡每天租车一次.已知甲、乙不超过两小时还车的概率分别为$\frac{1}{4}$,$\frac{1}{2}$;两小时以上且不超过三小时还车的概率分别为$\frac{1}{2}$,$\frac{1}{4}$;两人租车时间都不会超过四小时.(Ⅰ)分别求出甲、乙两人某一天在三小时以上且不超过四小时还车的概率.
(Ⅱ)记甲、乙两人一天所付的租车费用之和为ξ,求ξ的分布列及数学期望.
分析 (Ⅰ)根据题意,由全部基本事件的概率之和为1,利用对立事件概率计算公式求解即可.
(Ⅱ)由题意ξ的可能取值为0,2,4,6,8,分别求出相应的概率,由此能求出ξ的分布列及数学期望.
解答 解:(Ⅰ)甲在三小时以上且不超过四小时还车的概率为1-$\frac{1}{4}-\frac{1}{2}$=$\frac{1}{4}$,
乙在三小时以上且不超过四小时还车的概率为1-$\frac{1}{4}-\frac{1}{2}$=$\frac{1}{4}$.
(Ⅱ)由已知得ξ的可能取值为0,2,4,6,8,
P(ξ=0)=$\frac{1}{4}×\frac{1}{2}$=$\frac{1}{8}$,
P(ξ=2)=$\frac{1}{4}×\frac{1}{4}+\frac{1}{2}×\frac{1}{2}$=$\frac{5}{16}$,
P(ξ=4)=$\frac{1}{2}×\frac{1}{4}+\frac{1}{4}(1-\frac{1}{2}-\frac{1}{4})+\frac{1}{2}(1-\frac{1}{4}-\frac{1}{2})$=$\frac{5}{16}$,
P(ξ=6)=$\frac{1}{2}(1-\frac{1}{2}-\frac{1}{4})$+$\frac{1}{4}(1-\frac{1}{4}-\frac{1}{2})$=$\frac{3}{16}$,
P(ξ=8)=(1-$\frac{1}{2}-\frac{1}{4}$)(1-$\frac{1}{4}-\frac{1}{2}$)=$\frac{1}{16}$,
∴ξ的分布列为:
| ξ | 0 | 2 | 4 | 6 | 8 |
| P | $\frac{1}{8}$ | $\frac{5}{16}$ | $\frac{5}{16}$ | $\frac{3}{16}$ | $\frac{1}{16}$ |
点评 本题考查独立事件和互斥事件的概率,考查利用所学知识解决问题的能力,是中档题.

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
4.如图,网格纸上小正方形的边长为1,粗实线画出的是某三棱锥的三视图,则该三棱锥的体积为( )
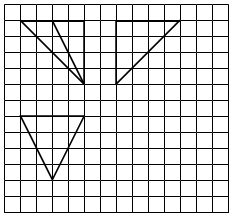

| A. | $\frac{16}{3}$ | B. | $\frac{{16\sqrt{3}}}{3}$ | C. | $\frac{32}{3}$ | D. | $\frac{64}{3}$ |
18.在等比数列{an}中,已知a4=27a3,则$\frac{{a}_{2}}{{a}_{1}}$+$\frac{{a}_{4}}{{a}_{2}}$+$\frac{{a}_{6}}{{a}_{3}}$+…+$\frac{{a}_{2n}}{{a}_{n}}$等于( )
| A. | $\frac{{3}^{-n}-3}{2}$ | B. | $\frac{{3}^{1-n}-3}{2}$ | C. | $\frac{{3}^{n}-3}{2}$ | D. | $\frac{{3}^{n+1}-3}{2}$ |
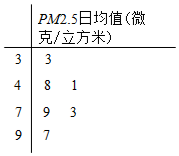 PM2.5是指大气中直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物.我国PM2.5标准采用世卫组织设定的最宽限值,PM2.5日均值在35微克/立方米以下空气质量为1级;在35微克/立方米~75微克/立方米之间空气质量为二级;在75微克/立方米及其以上空气质量为超标.
PM2.5是指大气中直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物.我国PM2.5标准采用世卫组织设定的最宽限值,PM2.5日均值在35微克/立方米以下空气质量为1级;在35微克/立方米~75微克/立方米之间空气质量为二级;在75微克/立方米及其以上空气质量为超标.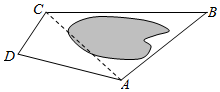 如图,为了测量A,C两点间的距离,选取同一平面上B、D两点,测出四边形ABCD各边的长度(单位:km):AB=5,BC=8,CD=3,DA=5,且∠B与∠D互补,则AC的长为7km.
如图,为了测量A,C两点间的距离,选取同一平面上B、D两点,测出四边形ABCD各边的长度(单位:km):AB=5,BC=8,CD=3,DA=5,且∠B与∠D互补,则AC的长为7km.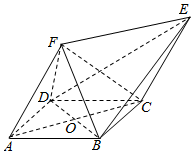 如图所示的几何体中,ABCD为菱形,ACEF为平行四边形,△BDF为等边三角形,O为AC与BD的交点.
如图所示的几何体中,ABCD为菱形,ACEF为平行四边形,△BDF为等边三角形,O为AC与BD的交点.