题目内容
已知数列{an}满足首项为a1=2,an+1=2an(n∈N*).设bn=3log2an-2(n∈N*),数列{cn}满足cn=anbn.
(Ⅰ)求证:数列{bn}成等差数列;
(Ⅱ)求数列{cn}的前n项和Sn.
(Ⅰ)求证:数列{bn}成等差数列;
(Ⅱ)求数列{cn}的前n项和Sn.
考点:数列的求和,等差关系的确定
专题:等差数列与等比数列
分析:(Ⅰ)由数列{an}的递推式求出{an}的通项公式,代入bn=3log2an-2整理,然后利用等差数列的定义证明数列{bn}成等差数列;
(Ⅱ)直接利用错位相减法求数列{cn}的前n项和Sn.
(Ⅱ)直接利用错位相减法求数列{cn}的前n项和Sn.
解答:
(Ⅰ)证明:∵an+1=2an,且a1=2≠0,
∴数列{an}为等比数列,则an=a1qn-1=2n,
∴bn=3log2an-2=3log22n-2=3n-2.
∵bn+1-bn=3(n+1)-2-3n+2=3,
∴{bn}为以3为公差的等差数列;
(Ⅱ)解:∵cn=anbn=(3n-2)•2n,
∴Sn=1•2+4•22+7•23+…+(3n-2)•2n ①
2Sn=1•22+4•23+7•24+…+(3n-5)•2n+(3n-2)•2n+1 ②
①-②得:-Sn=2+3[22+23+24+…+2n]-(3n-2)•2n+1
=2+3•
-(3n-2)•2n+1=-10+(5-3n)•2n+1,
∴Sn=10-(5-3n)•2n+1.
∴数列{an}为等比数列,则an=a1qn-1=2n,
∴bn=3log2an-2=3log22n-2=3n-2.
∵bn+1-bn=3(n+1)-2-3n+2=3,
∴{bn}为以3为公差的等差数列;
(Ⅱ)解:∵cn=anbn=(3n-2)•2n,
∴Sn=1•2+4•22+7•23+…+(3n-2)•2n ①
2Sn=1•22+4•23+7•24+…+(3n-5)•2n+(3n-2)•2n+1 ②
①-②得:-Sn=2+3[22+23+24+…+2n]-(3n-2)•2n+1
=2+3•
| 4(1-2n-1) |
| 1-2 |
∴Sn=10-(5-3n)•2n+1.
点评:本题考查了等差关系的确定,考查了数列的求和方法,训练了利用错位相减法求数列的和,是中档题.

练习册系列答案
相关题目
下列函数中周期为π且图象关于直线x=
对称的函数是( )
| π |
| 3 |
A、y=2sin(
| ||||
B、y=2sin(2x-
| ||||
C、y=2sin(2x+
| ||||
D、y=2sin(
|
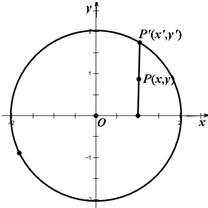 如图,将圆p:x2+y2=4上任意一点P′的纵坐标变为原来的一半 (横坐标不变),得到点P,并设点P的轨迹为曲线C.
如图,将圆p:x2+y2=4上任意一点P′的纵坐标变为原来的一半 (横坐标不变),得到点P,并设点P的轨迹为曲线C. 若F1、F2分别是椭圆
若F1、F2分别是椭圆