题目内容
椭圆C:
+
=1(a>b>0),点A为左顶点,点B为上顶点,直线AB的斜率为
,又直线y=k(x-1)经过椭圆C的一个焦点且与其相交于点M,N.
(Ⅰ)求椭圆C的方程;
(Ⅱ)将|MN|表示为k的函数;
(Ⅲ)线段MN的垂直平分线与x轴相交于点P,又点Q(1,0),求证:
为定值.
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
(Ⅰ)求椭圆C的方程;
(Ⅱ)将|MN|表示为k的函数;
(Ⅲ)线段MN的垂直平分线与x轴相交于点P,又点Q(1,0),求证:
| |PQ| |
| |MN| |
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线的定义、性质与方程
分析:(Ⅰ)由直线AB的斜率为
得到
=
,求直线经过的定点得椭圆焦点,结合a2=b2+c2求得a2,b2的值,则椭圆方程可求;
(Ⅱ)联立直线和椭圆方程,化为关于x的一元二次方程,由弦长公式得到|MN|关于k的函数;
(Ⅲ)求出线段MN的垂直平分线方程,取y=0求得P点坐标,则|PQ|可求,直接作比得到
为定值.
| ||
| 2 |
| b |
| a |
| ||
| 2 |
(Ⅱ)联立直线和椭圆方程,化为关于x的一元二次方程,由弦长公式得到|MN|关于k的函数;
(Ⅲ)求出线段MN的垂直平分线方程,取y=0求得P点坐标,则|PQ|可求,直接作比得到
| |PQ| |
| |MN| |
解答:
(Ⅰ)解:如图,
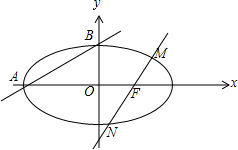
∵直线AB的斜率为
,
∴
=
,
又直线y=k(x-1)经过椭圆C的一个焦点,
∴交点F(1,0).
则
,解得a2=4,b2=3.
∴椭圆C的方程为
+
=1;
(Ⅱ)解:联立
,得(3+4k2)x2-8k2x+4k2-12=0.
设M(x1,y1),N(x2,y2),
则x1+x2=
,x1x2=
.
∴|MN|=
=
=
.
(Ⅲ)证明:线段MN的中点的横坐标为
=
,纵坐标为k•(
-1)=
.
∴线段MN的垂直平分线方程为y+
=-
(x-
),
取y=0,得x=
,
∴P(
,0),
则|PQ|=1-
=
.
则
=
=
为定值.

∵直线AB的斜率为
| ||
| 2 |
∴
| b |
| a |
| ||
| 2 |
又直线y=k(x-1)经过椭圆C的一个焦点,
∴交点F(1,0).
则
|
∴椭圆C的方程为
| x2 |
| 4 |
| y2 |
| 3 |
(Ⅱ)解:联立
|
设M(x1,y1),N(x2,y2),
则x1+x2=
| 8k2 |
| 3+4k2 |
| 4k2-12 |
| 3+4k2 |
∴|MN|=
| 1+k2 |
| (x1+x2)2-4x1x2 |
=
| 1+k2 |
(
|
| 12(1+k2) |
| 3+4k2 |
(Ⅲ)证明:线段MN的中点的横坐标为
| x1+x2 |
| 2 |
| 4k2 |
| 3+4k2 |
| 4k2 |
| 3+4k2 |
| -3k |
| 3+4k2 |
∴线段MN的垂直平分线方程为y+
| 3k |
| 3+4k2 |
| 1 |
| k |
| 4k2 |
| 3+4k2 |
取y=0,得x=
| k2 |
| 3+4k2 |
∴P(
| k2 |
| 3+4k2 |
则|PQ|=1-
| k2 |
| 3+4k2 |
| 3(1+k2) |
| 3+4k2 |
则
| |PQ| |
| |MN| |
| ||
|
| 1 |
| 4 |
点评:本题主要考查椭圆方程的求法,考查了直线与椭圆的位置关系的应用,直线与曲线联立,根据方程的根与系数的关系解题,是处理这类问题的最为常用的方法,考查了弦长公式的应用,训练了学生的运算能力,属难题.

练习册系列答案
相关题目
下列函数中周期为π且图象关于直线x=
对称的函数是( )
| π |
| 3 |
A、y=2sin(
| ||||
B、y=2sin(2x-
| ||||
C、y=2sin(2x+
| ||||
D、y=2sin(
|
执行如图所示的程序框图,则输出S的值是( )


| A、10 | B、17 | C、26 | D、28 |
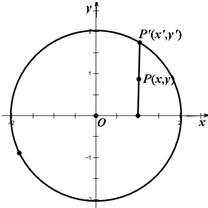 如图,将圆p:x2+y2=4上任意一点P′的纵坐标变为原来的一半 (横坐标不变),得到点P,并设点P的轨迹为曲线C.
如图,将圆p:x2+y2=4上任意一点P′的纵坐标变为原来的一半 (横坐标不变),得到点P,并设点P的轨迹为曲线C.