题目内容
13.(1)已知实数x,y均为正数,求证:$(x+y)(\frac{4}{x}+\frac{9}{y})≥25$;(2)解关于x的不等式x2-2ax+a2-1<0(a∈R).
分析 (1)化简不等式的左边,利用基本不等式求得最小值即可;
(2)原不等式可化为[x-(a+1)]•[x-(a-1)]<0,求出不等式对应方程的根,再写出不等式的解集.
解答 解:(1)证明:$(x+y)(\frac{4}{x}+\frac{9}{y})=4+9+\frac{4y}{x}+\frac{9x}{y}$=$13+(\frac{4y}{x}+\frac{9x}{y})$,…(2分)
又因为x>0,y>0,所以$\frac{4y}{x}>0,\frac{9x}{y}>0$,
由基本不等式得,$\frac{4y}{x}+\frac{9x}{y}≥2\sqrt{\frac{4y}{x}•\frac{9x}{y}}=12$,…(4分)
当且仅当$\frac{4y}{x}=\frac{9x}{y}$时,取等号,
即2y=3x时取等号,
所以$(x+y)(\frac{4}{x}+\frac{9}{y})≥25$;…(5分)
(2)原不等式可化为[x-(a+1)]•[x-(a-1)]<0,…(7分)
令[x-(a+1)]•[x-(a-1)]=0,
得 x1=a+1,x2=a-1,
又因为a+1>a-1,…(9分)
所以原不等式的解集为(a-1,a+1).…(10分)
点评 本题考查了基本不等式与一元二次不等式的解法和应用问题,是中档题.

练习册系列答案
相关题目
3.函数f(x)=cos(3x+φ)的图象关于原点成中心对称,则φ等于( )
| A. | -$\frac{π}{2}$ | B. | 2kπ-$\frac{π}{2}$(k∈Z) | C. | kπ(k∈Z) | D. | kπ+$\frac{π}{2}$(k∈Z) |
4.函数f(x)=x2-2x-1,x∈[-3,2]的最大值、最小值分别为( )
| A. | 14,-2 | B. | 14,-1 | C. | 2,-2 | D. | 7,-2 |
1.如图所示,在△ABC中,BD=2CD,若$\overrightarrow{AB}=\overrightarrow a$,$\overrightarrow{AC}=\overrightarrow b$,则$\overrightarrow{AD}$=( )
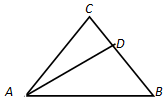

| A. | $\frac{2}{3}\overrightarrow a+\frac{1}{3}\overrightarrow b$ | B. | $\frac{2}{3}\overrightarrow a-\frac{1}{3}\overrightarrow b$ | C. | $\frac{1}{3}\overrightarrow a+\frac{2}{3}\overrightarrow b$ | D. | $\frac{2}{3}\overrightarrow a-\frac{2}{3}\overrightarrow b$ |
8.复数z满足z(1-2i)=3+4i复数z的共轭复数所对应的点在第( )象限.
| A. | 一 | B. | 二 | C. | 三 | D. | 四 |
5.已知△ABC中,内角A,B,C的对边分别为a,b,c,若a2=b2+c2-bc,a=4,则△ABC的外接圆半径为( )
| A. | $\frac{{4\sqrt{3}}}{3}$ | B. | $\frac{{8\sqrt{3}}}{3}$ | C. | 4 | D. | 8 |