题目内容

6．若x0是函数f（x）=-x3-3x+5的零点，则x0所在的一个区间是（　　）
A．（0，1）B．（1，2）C．（2，3）D．（3，4）

分析 判断函数的连续性，利用零点判定定理求解即可．

解答 解：函数f（x）=-x3-3x+5是连续函数，
因为f（1）=1＞0，f（2）=-8-6+5＜0，
可知f（1）f（2）＜0，
由零点判定定理可知，函数的零点x0所在的一个区间是（1，2）．
故选：B．

点评 本题考查函数的零点判定定理的应用，考查计算能力．

练习册系列答案
相关题目
16．已知$f（x）=sin（{2x-\frac{π}{6}}）-cos（{2x+\frac{π}{3}}）+a$
（1）把y=f（x）图象上所有点的横坐标伸长到原来的2倍（纵坐标不变），再把所得图象上所有点向左平行移动$\frac{π}{3}$个单位长度，得到y=g（x）的图象，求函数y=g（x）的解析式；
（2）y=g（x）在$[0，\frac{π}{2}]$上最大值与最小值之和为5，求a的值．
17．以下给出关于向量的四个结论：
①$\overrightarrow a•\overrightarrow b-\overrightarrow b•\overrightarrow a=0$；     
②$（\overrightarrow a+\overrightarrow b）•\overrightarrow c=\overrightarrow a•\overrightarrow c+\overrightarrow b•\overrightarrow c$；     
③$|\overrightarrow a•\overrightarrow b|=|\overrightarrow a|•|\overrightarrow b|$；
④若$|\overrightarrow a|≠|\overrightarrow b|$，则$\overrightarrow a≠\overrightarrow b$；
其中正确结论的序号是①②④．
14．已知$\frac{tanα}{tanα-1}$=-1，求下列各式的值．
（Ⅰ）$\frac{sinα-3cosα}{sinα+2cosα}$l；
（Ⅱ）$\frac{sin（π-α）cos（π+α）cos（\frac{π}{2}+α）cos（\frac{π}{2}-α）}{cos（π-α）sin（3π-α）sin（-π-α）sin（\frac{π}{2}+α）}$．
1．已知全集U={1，2，3，4，5}，A={1，3}，B={2，4}，则∁U（A∪B）=（　　）
A．5B．{5}C．∅D．{1，2，3，4}
11．已知函数y=sinx（x∈[m，n]），值域为$[-\frac{1}{2}，1]$，则n-m的最大值为$\frac{4π}{3}$，最小值为$\frac{2π}{3}$．
18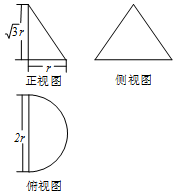．若一个空间几何体的三视图如图所示，且已知该几何体的体积为$\frac{\sqrt{3}}{6}π$，则其表面积为（　　）
A．$\frac{3}{2}π+\sqrt{3}$B．$\frac{3}{2}π$C．$\frac{3}{4}π+2\sqrt{3}$D．$\frac{3}{4}π+\sqrt{3}$
15．设实数x、y满足4x2-2$\sqrt{3}$xy+4y2=13，则x2+4y2的取值范围是$[10-4\sqrt{3}，10+4\sqrt{3}]$．
16．已知命题p：-x2+8x+20≥0；命题q：x2+2x+1-4m2≤0．
（1）当m∈R时，解不等式x2+2x+1-4m2≤0；
（2）当m＞0时，若￢p是￢q的必要不充分条件，求实数m的取值范围．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网