题目内容
17．以下给出关于向量的四个结论：①$\overrightarrow a•\overrightarrow b-\overrightarrow b•\overrightarrow a=0$；
②$（\overrightarrow a+\overrightarrow b）•\overrightarrow c=\overrightarrow a•\overrightarrow c+\overrightarrow b•\overrightarrow c$；
③$|\overrightarrow a•\overrightarrow b|=|\overrightarrow a|•|\overrightarrow b|$；
④若$|\overrightarrow a|≠|\overrightarrow b|$，则$\overrightarrow a≠\overrightarrow b$；
其中正确结论的序号是①②④．
分析 利用向量的数量积以及向量的模的运算法则化简求解判断即可．
解答 解：①$\overrightarrow a•\overrightarrow b-\overrightarrow b•\overrightarrow a=0$；满足向量的数量积的运算法则，正确；
②$（\overrightarrow a+\overrightarrow b）•\overrightarrow c=\overrightarrow a•\overrightarrow c+\overrightarrow b•\overrightarrow c$；满足向量的数量积的运算法则，正确；
③$|\overrightarrow a•\overrightarrow b|=|\overrightarrow a|•|\overrightarrow b|$；不满足数量积的运算法则，所以不正确；
④若$|\overrightarrow a|≠|\overrightarrow b|$，则$\overrightarrow a≠\overrightarrow b$；正确．
故答案为：①②④
点评 本题考查向量的数量积的运算法则的应用，是基础题．
练习册系列答案
教材全解字词句篇系列答案
相关题目
7．已知某几何体的三视图如图所示，则其体积为（ ）
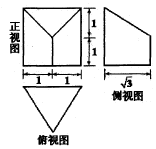
| A． | $2\sqrt{3}$ | B． | $\frac{{5\sqrt{3}}}{3}$ | C． | $\sqrt{3}$ | D． | $\frac{{\sqrt{3}}}{3}$ |
5．设$a={3^{\frac{1}{3}}}，b={（\frac{1}{4}）^{3.1}}，c={log_{0.4}}3$，则a，b，c的大小关系为（ ）
| A． | c＜a＜b | B． | c＜b＜a | C． | b＜a＜c | D． | a＜b＜c |
12．假设行列式的计算公式：$|\begin{array}{l}{a}&{b}\\{c}&{d}\end{array}|$=ad-bc，若f（x）=$|\begin{array}{l}{x}&{x}\\{3}&{{x}^{2}}\end{array}|$，则函数f（x）的单调减区间为（ ）
| A． | $（-\sqrt{3}，\sqrt{3}）$ | B． | （-1，1） | C． | $（-\sqrt{2}，\sqrt{2}）$ | D． | （-2，2） |
2．设集合A={1，2，3}，B={2，3}，则A∪B=（ ）
| A． | {2} | B． | {3} | C． | {2} | D． | {1，2，3} |
6．若x0是函数f（x）=-x3-3x+5的零点，则x0所在的一个区间是（ ）
| A． | （0，1） | B． | （1，2） | C． | （2，3） | D． | （3，4） |
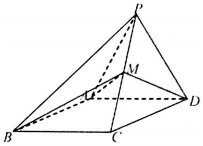如图所示，四棱锥P-ABCD的侧面PAD是边长为2的正三角形，底面ABCD是∠ABC=60°的菱形，M为PC的中点，PC=$\sqrt{6}$．