题目内容
16.已知$f(x)=sin({2x-\frac{π}{6}})-cos({2x+\frac{π}{3}})+a$(1)把y=f(x)图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),再把所得图象上所有点向左平行移动$\frac{π}{3}$个单位长度,得到y=g(x)的图象,求函数y=g(x)的解析式;
(2)y=g(x)在$[0,\frac{π}{2}]$上最大值与最小值之和为5,求a的值.
分析 (1)利用诱导公式,函数y=Asin(ωx+φ)的图象变换规律,求得g(x)的解析式.
(2)利用正弦函数的图象的定义域和值域,求得函数g(x)的最值,利用条件求得a的值.
解答 解:(1)把y=f(x)=sin(2x-$\frac{π}{6}$)-cos(2x+$\frac{π}{3}$)+a=sin(2x-$\frac{π}{6}$)-sin($\frac{π}{6}$-2x)+a=2sin(2x-$\frac{π}{6}$)+a的图象上所有点的横坐标,
伸长到原来的2倍(纵坐标不变),可得y=2sin(x-$\frac{π}{6}$)+a的图象,
把所得图象上所有点向左平行移动$\frac{π}{3}$个单位长度,得到y=g(x)=2sin(x+$\frac{π}{3}$-$\frac{π}{6}$)+a=2sin(x+$\frac{π}{6}$)+a 的图象,
故函数y=g(x)的解析式为 g(x)=2sin(x+$\frac{π}{6}$)+a.
(2)∵在$[0,\frac{π}{2}]$上,x+$\frac{π}{6}$∈[$\frac{π}{6}$,$\frac{2π}{3}$],sin(x+$\frac{π}{6}$)∈[$\frac{1}{2}$,1],∴g(x)∈[1+a,2+a],
根据g(x)的最大值与最小值之和为5,∴1+a+2+a=5,a=1.
点评 本题主要考查诱导公式,函数y=Asin(ωx+φ)的图象变换规律,正弦函数的图象的定义域和值域,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
6.已知直线l的方向向量为$\vec s=(1,2,x)$,平面α的法向量$\vec n=(-2,y,2)$,若l?α,则xy的最大值为( )
| A. | 1 | B. | $\frac{1}{4}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{8}$ |
7.已知某几何体的三视图如图所示,则其体积为( )
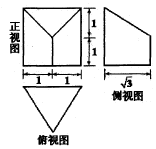

| A. | $2\sqrt{3}$ | B. | $\frac{{5\sqrt{3}}}{3}$ | C. | $\sqrt{3}$ | D. | $\frac{{\sqrt{3}}}{3}$ |
5.设$a={3^{\frac{1}{3}}},b={(\frac{1}{4})^{3.1}},c={log_{0.4}}3$,则a,b,c的大小关系为( )
| A. | c<a<b | B. | c<b<a | C. | b<a<c | D. | a<b<c |
6.若x0是函数f(x)=-x3-3x+5的零点,则x0所在的一个区间是( )
| A. | (0,1) | B. | (1,2) | C. | (2,3) | D. | (3,4) |