题目内容
15.设实数x、y满足4x2-2$\sqrt{3}$xy+4y2=13,则x2+4y2的取值范围是$[10-4\sqrt{3},10+4\sqrt{3}]$.分析 设x2+4y2=t2,则x=tcosα,y=$\frac{1}{2}$tsinα,代入4x2-2$\sqrt{3}$xy+4y2=13,可得t2=$\frac{13}{4co{s}^{2}α-\sqrt{3}sinαcosα+si{n}^{2}α}$=$\frac{13}{\frac{5}{2}-\sqrt{3}sin(2α-\frac{π}{3})}$,利用三角函数的单调性即可得出.
解答 解:设x2+4y2=t2,则x=tcosα,y=$\frac{1}{2}$tsinα,
∵4x2-2$\sqrt{3}$xy+4y2=13,
∴t2=$\frac{13}{4co{s}^{2}α-\sqrt{3}sinαcosα+si{n}^{2}α}$=$\frac{13}{3×\frac{1+cos2α}{2}-\frac{\sqrt{3}}{2}sinαcosα+1}$=$\frac{13}{\frac{5}{2}+\sqrt{3}(\frac{\sqrt{3}}{2}cos2α-\frac{1}{2}sin2α)}$=$\frac{13}{\frac{5}{2}-\sqrt{3}sin(2α-\frac{π}{3})}$,
∴$sin(2α-\frac{π}{3})$=-1时,t2取得最小值:$\frac{13}{\frac{5}{2}+\sqrt{3}}$=10-4$\sqrt{3}$;
$sin(2α-\frac{π}{3})$=1时,t2取得最大值:$\frac{13}{\frac{5}{2}-\sqrt{3}}$=10+4$\sqrt{3}$.
综上可得:t2∈$[10-4\sqrt{3},10+4\sqrt{3}]$.
即x2+4y2的取值范围是$[10-4\sqrt{3},10+4\sqrt{3}]$.
故答案为:$[10-4\sqrt{3},10+4\sqrt{3}]$.
点评 本题考查了三角函数的单调性与值域、换元方法、函数的单调性,考查了推理能力与计算能力,属于难题.

| A. | c<a<b | B. | c<b<a | C. | b<a<c | D. | a<b<c |
| A. | (0,1) | B. | (1,2) | C. | (2,3) | D. | (3,4) |
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 2 | D. | 3 |
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
 如图,抛物线C:y2=2px的焦点为F,抛物线上一定点Q(1,2).
如图,抛物线C:y2=2px的焦点为F,抛物线上一定点Q(1,2).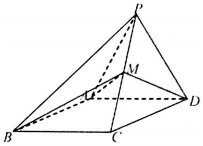 如图所示,四棱锥P-ABCD的侧面PAD是边长为2的正三角形,底面ABCD是∠ABC=60°的菱形,M为PC的中点,PC=$\sqrt{6}$.
如图所示,四棱锥P-ABCD的侧面PAD是边长为2的正三角形,底面ABCD是∠ABC=60°的菱形,M为PC的中点,PC=$\sqrt{6}$.