题目内容
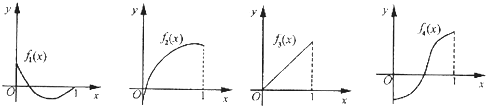
如图所示,fi(x)(i=1,2,3,4)是定义在[0,1]上的四个函数,其中满足性质:“对[0,1]中任意的x1和x2,任意λ∈[0.1],f[λx1+(1-λ)x2]≤λf(x1)+(1-λ)f(x2)恒成立”的只有( )

| A、f1(x),f3(x) |
| B、f2(x) |
| C、f2(x),f3(x) |
| D、f4(x) |
考点:函数的图象
专题:函数的性质及应用
分析:由题设对[0,1]中任意的x1和x2,任意λ∈[0,1],f[λx1+(1-λ)x2]≤λf(x1)+(1-λ)f(x2)恒成立,知,此函数必不为一凹函数,依据凹函数的图象特征进行判断即可.
解答:
解:由题意,观察四个选项:f1(x)中的图象先降后升是一凸函数,满足要求,
f2(x)中的函数是先升后降是一凹函数,不满足要求;
f3(x)中的图象直线上升,不是凹函数,满足要求,
f4(x)中的函数图象凸、凹函数各一部分.不满足要求;
考察定义:对[0,1]中任意的x1和x2,任意λ∈[0,1],f[λx1+(1-λ)x2]≤λf(x1)+(1-λ)f(x2)恒成立知,此函数在[0,1]不是凹函数,由上分析知只有f1(x),f3(x)符合题意.
故选:A.
f2(x)中的函数是先升后降是一凹函数,不满足要求;
f3(x)中的图象直线上升,不是凹函数,满足要求,
f4(x)中的函数图象凸、凹函数各一部分.不满足要求;
考察定义:对[0,1]中任意的x1和x2,任意λ∈[0,1],f[λx1+(1-λ)x2]≤λf(x1)+(1-λ)f(x2)恒成立知,此函数在[0,1]不是凹函数,由上分析知只有f1(x),f3(x)符合题意.
故选:A.
点评:本题的考点是函数的图象,考查函数图象的变化规律,在本题中给出了一个新定义,对于新定义的题型,要认真研究其运算特征,充分理解其内涵再依据新规则做题.

练习册系列答案
相关题目
三棱锥的三个侧面都是直角三角形,且三个直角的顶点恰是三棱锥的顶点,则其底面一定是( )
| A、直角三角形 |
| B、钝角三角形 |
| C、锐角三角形 |
| D、等边三角形 |
设
=(-2,1-cosθ),
=(1+cosθ,-
),且
∥
,则锐角θ=( )
| a |
| b |
| 1 |
| 4 |
| a |
| b |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
当x≠0时,有不等式( )
| A、ex<1+x |
| B、当x>0时,ex<1+x;当x<0时,ex>1+x |
| C、ex>1+x |
| D、当x<0时,ex<1+x;当x>0时,ex<1+x |
阅读右侧程序框图,输出结果S的值为( )


A、
| ||||
B、
| ||||
C、-
| ||||
D、
|
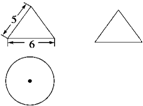 有一个几何体的三视图及其尺寸如图所示(单位:cm),则该几何体的表面积及体积为( )
有一个几何体的三视图及其尺寸如图所示(单位:cm),则该几何体的表面积及体积为( )| A、24π cm2,12π cm3 |
| B、15π cm2,12π cm3 |
| C、24π cm2,36π cm3 |
| D、以上都不正确 |
已知函数f(x)=sinx-lnx(0<x<2π)的零点为x0有0<a<b<c<2π使f(a)f(b)f(c)>0则下列结论不可能成立的是( )
| A、x0<a |
| B、x0>b |
| C、x0>c |
| D、x0<π |