题目内容
已知函数f（x）=sinx-lnx（0＜x＜2π）的零点为x0有0＜a＜b＜c＜2π使f（a）f（b）f（c）＞0则下列结论不可能成立的是（ ）
| A、x0＜a |
| B、x0＞b |
| C、x0＞c |
| D、x0＜π |
考点：函数零点的判定定理
专题：计算题,作图题,函数的性质及应用
分析：由题意判断f（x）的正负，进而求出零点可能的范围．
解答：
解：由右图可知，
函数f（x）=sinx-lnx（0＜x＜2π）先正后负，
则由有0＜a＜b＜c＜2π使f（a）f（b）f（c）＞0可知，
f（a）＞0，f（b）＜0，f（c）＜0或f（a）＞0，f（b）＞0，f（c）＞0，
则x0＜a不可能；
故选 A．
函数f（x）=sinx-lnx（0＜x＜2π）先正后负，
则由有0＜a＜b＜c＜2π使f（a）f（b）f（c）＞0可知，
f（a）＞0，f（b）＜0，f（c）＜0或f（a）＞0，f（b）＞0，f（c）＞0，
则x0＜a不可能；
故选 A．
点评：本题考查了函数的零点的判断，属于基础题．
练习册系列答案
相关题目
5人站成一排，甲、乙两人之间恰有1人的不同站法的种数为（ ）
| A、18 | B、24 | C、36 | D、48 |
如图所示，fi（x）（i=1，2，3，4）是定义在[0，1]上的四个函数，其中满足性质：“对[0，1]中任意的x1和x2，任意λ∈[0.1]，f[λx1+（1-λ）x2]≤λf（x1）+（1-λ）f（x2）恒成立”的只有（ ）
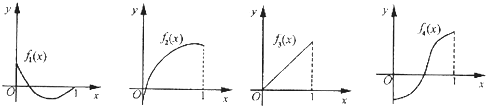
| A、f1（x），f3（x） |
| B、f2（x） |
| C、f2（x），f3（x） |
| D、f4（x） |
f（x）=lnx+x2-3x的极大值点是（ ）
A、
| ||
| B、1 | ||
| C、2 | ||
| D、3 |
函数f（x）=
的零点个数为（ ）
|
| A、1个 | B、2个 | C、3个 | D、4个 |
国庆节放假，甲、乙、丙去北京旅游的概率分别是
，
，
．假定三人的行动相互之间没有影响，那么这段时间内至少有1人去北京旅游的概率为（ ）
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 5 |
A、
| ||
B、
| ||
C、
| ||
D、
|