题目内容
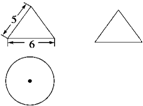有一个几何体的三视图及其尺寸如图所示（单位：cm），则该几何体的表面积及体积为（ ）| A、24π cm2，12π cm3 |
| B、15π cm2，12π cm3 |
| C、24π cm2，36π cm3 |
| D、以上都不正确 |
考点：由三视图求面积、体积
专题：计算题,空间位置关系与距离
分析：由三视图想象出空间几何体，代入数值即可．
解答：
解：由三视图可知，
该几何体是圆锥，
底面半径为3，母线长为5，高为4．
故其表面积为π×32+π×3×5=24π（cm2），
其体积为
×π×32×4=12π（cm3）；
故选A．
该几何体是圆锥，
底面半径为3，母线长为5，高为4．
故其表面积为π×32+π×3×5=24π（cm2），
其体积为
| 1 |
| 3 |
故选A．
点评：本题考查了学生的空间想象力，属于基础题．
练习册系列答案
培优三好生系列答案
相关题目
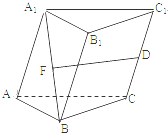在三棱柱ABC-A1B1C1中，D是CC1的中点，F是A1B的中点，且| DF |
| AB |
| AC |
A、α=
| ||
B、α=-
| ||
C、α=1，β=-
| ||
D、α=-1，β=
|
M={1，2，3，4，5}在M到M上的一一映射中，至少有两个数字与自身对应的映射个数为（ ）
| A、35 | B、31 | C、41 | D、21 |
如图所示，fi（x）（i=1，2，3，4）是定义在[0，1]上的四个函数，其中满足性质：“对[0，1]中任意的x1和x2，任意λ∈[0.1]，f[λx1+（1-λ）x2]≤λf（x1）+（1-λ）f（x2）恒成立”的只有（ ）
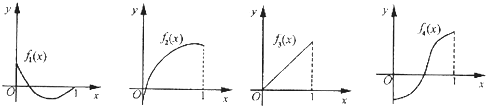
| A、f1（x），f3（x） |
| B、f2（x） |
| C、f2（x），f3（x） |
| D、f4（x） |
在锐角三角形中，a、b、c分别是内角A、B、C的对边，设B=2A，则
的取值范围是（ ）
| b |
| a |
| A、（-2，2） | ||||
| B、（0，2） | ||||
C、（
| ||||
D、（
|
f（x）=lnx+x2-3x的极大值点是（ ）
A、
| ||
| B、1 | ||
| C、2 | ||
| D、3 |
函数f（x）=
的零点个数为（ ）
|
| A、1个 | B、2个 | C、3个 | D、4个 |