题目内容
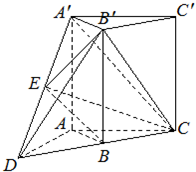 如图,直三棱柱A′B′C′-ABC,延长CB到点D,使BD=BC,点E为A′D的中点,∠ABC=90°,AB=BC=
如图,直三棱柱A′B′C′-ABC,延长CB到点D,使BD=BC,点E为A′D的中点,∠ABC=90°,AB=BC=| 2 |
(Ⅰ)证明:BE∥平面A′ACC′;
(Ⅱ)求三棱锥A′-EB′C的体积.
考点:棱柱、棱锥、棱台的体积,直线与平面平行的判定
专题:综合题,空间位置关系与距离
分析:(Ⅰ)证明BE∥A′C,即可证明BE∥平面A′ACC′;
(Ⅱ)转换底面求三棱锥A′-EB′C的体积.
(Ⅱ)转换底面求三棱锥A′-EB′C的体积.
解答:
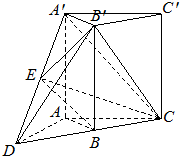 (Ⅰ)证明:∵E、B分别为A′D、DC的中点,
(Ⅰ)证明:∵E、B分别为A′D、DC的中点,
∴BE∥A′C …(2分)
又A′C?平面A′ACC′,且BE?平面A′ACC′,
∴BE∥平面A′ACC′. …(6分)
(Ⅱ)解:∵AB=BC=
, ∠ABC=90° , ∴AC=A′A=2,
∵ABC-A'B'C'为直三棱柱,∴∠A'B'C'=90°,∴A'B'⊥B'C',
又BB'⊥平面A'B'C',∴A'B'⊥B'B
∴A'B'⊥平面BCC'B'.…(8分)
∴VA′-EB′C=VB′-A′EC=
VB′-A′DC=
VA′-B′DC. …(10分)
=
[
×(
×2
×2)
]=
.…(12分)
 (Ⅰ)证明:∵E、B分别为A′D、DC的中点,
(Ⅰ)证明:∵E、B分别为A′D、DC的中点,∴BE∥A′C …(2分)
又A′C?平面A′ACC′,且BE?平面A′ACC′,
∴BE∥平面A′ACC′. …(6分)
(Ⅱ)解:∵AB=BC=
| 2 |
∵ABC-A'B'C'为直三棱柱,∴∠A'B'C'=90°,∴A'B'⊥B'C',
又BB'⊥平面A'B'C',∴A'B'⊥B'B
∴A'B'⊥平面BCC'B'.…(8分)
∴VA′-EB′C=VB′-A′EC=
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| 2 |
| 2 |
| 2 |
| 3 |
点评:本题考查线面平行,考查三棱锥A′-EB′C的体积,正确运用线面平行的判定定理是关键.

练习册系列答案
相关题目
命题“若α=
,则tanα=1”的逆否命题是( )
| π |
| 4 |
A、若tanα≠1,则α≠
| ||
B、若α=
| ||
C、若α≠
| ||
D、若tanα≠1,则α=
|
 如图,以摩天轮中心为原点,水平方向为x轴建立平面直角坐标系,动点初始位于点P0(4,-3)处,现将其绕原点O逆时针旋转120°角到达点P处,则此时点P的纵坐标为
如图,以摩天轮中心为原点,水平方向为x轴建立平面直角坐标系,动点初始位于点P0(4,-3)处,现将其绕原点O逆时针旋转120°角到达点P处,则此时点P的纵坐标为