题目内容
若在区间[0,1]上存在实数x使2x(3x+a)<1成立,则a的取值范围是 .
考点:函数恒成立问题
专题:计算题,函数的性质及应用,不等式的解法及应用
分析:2x(3x+a)<1可化为a<2-x-3x,则在区间[0,1]上存在实数x使2x(3x+a)<1成立,等价于a<(2-x-3x)max,利用函数的单调性可求最值.
解答:
解:2x(3x+a)<1可化为a<2-x-3x,
则在区间[0,1]上存在实数x使2x(3x+a)<1成立,等价于a<(2-x-3x)max,
而2-x-3x在[0,1]上单调递减,
∴2-x-3x的最大值为20-0=1,
∴a<1,
故a的取值范围是(-∞,1),
故答案为:(-∞,1).
则在区间[0,1]上存在实数x使2x(3x+a)<1成立,等价于a<(2-x-3x)max,
而2-x-3x在[0,1]上单调递减,
∴2-x-3x的最大值为20-0=1,
∴a<1,
故a的取值范围是(-∞,1),
故答案为:(-∞,1).
点评:该题考查函数恒成立问题,考查转化思想,注意“存在”与“恒成立”问题的区别与联系是解题关键.

练习册系列答案
 全能练考卷系列答案
全能练考卷系列答案
相关题目
已知x,y满足约束条件
若目标函数z=2x+y的最小值为-2014,则a的值为( )
|
| A、1008 | B、1006 |
| C、-1008 | D、-1006 |
设△ABC的内角A,B,C所对的边分别是a,b,c,若sinA,sinC,sinB成等差数列,且3c=5a,则角B=( )
A、
| ||
B、
| ||
C、
| ||
D、
|
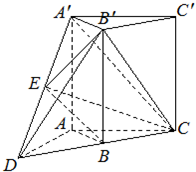 如图,直三棱柱A′B′C′-ABC,延长CB到点D,使BD=BC,点E为A′D的中点,∠ABC=90°,AB=BC=
如图,直三棱柱A′B′C′-ABC,延长CB到点D,使BD=BC,点E为A′D的中点,∠ABC=90°,AB=BC=