题目内容

抛物线y2=8x的焦点到直线x-
3
y=0的距离是
 
．
考点：抛物线的简单性质
专题：计算题,圆锥曲线的定义、性质与方程
分析：由抛物线y2=8x得焦点F（2，0），再利用点到直线的距离公式可得点F（2，0）到直线x-
3
y=0的距离．
解答： 解：由抛物线y2=8x得焦点F（2，0），
∴点F（2，0）到直线x-
3
y=0的距离d=
2
1+3
=1．
故答案为：1．
点评：熟练掌握抛物线的性质和点到直线的距离公式是解题的关键．
练习册系列答案
相关题目
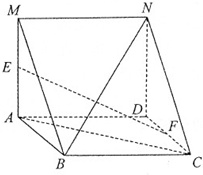如图，四边形ABCD是菱形，四边形MADN是矩形，平面MADN⊥平面ABCD，E，F分别为MA，DC的中点，求证：
（Ⅰ）EF∥平面MNCB；
（Ⅱ）平面MAC⊥平面BND．
已知椭圆E：
x2
a2
+
y2
b2
=1（a＞0，b＞0）的左、右焦点分别为F1、F2，正△PF1F2的中心恰为椭圆的上顶点A，且
AF1
•
AF2
=-2．
（1）求椭圆E的方程；
（2）过点P的直线l与椭圆E交于M，N两点，点B在x轴上，△BMN是以角B为顶角的等腰直角三角形，求直线l的方程．
在一次口试中，要从10道题中随机抽出3道题进行回答，答对其中两道或两道以上的题可获得及格．某考生会回答10道题中的6道题，那么他（她）获得及格的概率是
 
．
设a，b，c是△ABC中∠A，∠B，∠C的对边，a=2
3
，c=6，cosB=-
3
3
，则b=
 
；△ABC的面积为
 
．
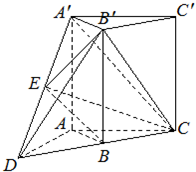如图，直三棱柱A′B′C′-ABC，延长CB到点D，使BD=BC，点E为A′D的中点，∠ABC=90°，AB=BC=
2
，A′A=2．
（Ⅰ）证明：BE∥平面A′ACC′；
（Ⅱ）求三棱锥A′-EB′C的体积．
定义在（0，+∞）上的函数f（x）满足：①当x∈[1，3）时，f（x）=
x-1，1≤x≤2
3-x，2＜x＜3
②f（3x）=3f（x），设关于x的函数F（x）=f（x）-1的零点从小到大依次记为x1，x2，x3，x4，x5，…，则x1+x2+x3+x4+x5=
 
．
已知⊙O：x2+y2=1，直线l：y=-1，则在⊙O上任取一点，该点到直线l的距离不小于
3
2
的概率是
 
．
极坐标系内曲线ρ=2cosθ上的动点P与定点Q（1，
π
2
），的最近距离等于（　　）
A、
2
-1
B、
5
-1
C、1
D、
2

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网