题目内容
已知数列{an}是首项a1=1的等比数列,其前n项和Sn中,S3,S4,S2成等差数列,求数列{an}的通项公式.
考点:等比数列的性质
专题:计算题,分类讨论,等差数列与等比数列
分析:讨论q=1,q≠1,两种情况,运用等差数列的性质和等比数列的求和公式,计算即可得到.
解答:
解:若q=1,则S3=3,S4=4,S2=2,
显然S3,S4,S2不成等差数列,
则q≠1,故由S3,S4,S2成等差数列,
则2•
=
+
,
则有2q4=q3+q2,即2q2-q-1=0,解得q=1(舍去)或q=-
,
则an=a1qn-1=(-
)n-1.
显然S3,S4,S2不成等差数列,
则q≠1,故由S3,S4,S2成等差数列,
则2•
| a1(1-q4) |
| 1-q |
| a1(1-q3) |
| 1-q |
| a1(1-q2) |
| 1-q |
则有2q4=q3+q2,即2q2-q-1=0,解得q=1(舍去)或q=-
| 1 |
| 2 |
则an=a1qn-1=(-
| 1 |
| 2 |
点评:本题考查等差数列的性质和等比数列的通项公式和求和公式,注意公比为1的情况,考查分类讨论的思想方法,考查运算能力,属于基础题.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
若数列的前4项分别是
,-
,
,-
,则此数列的一个通项公式为( )
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 5 |
A、
| ||
B、
| ||
C、
| ||
D、
|
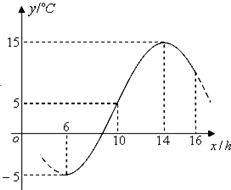 如图,某地一天6-16时的温度变化曲线近似满足函数y=Asin(ωx+φ)+b,其中A>0,ω>0,0<φ<π.
如图,某地一天6-16时的温度变化曲线近似满足函数y=Asin(ωx+φ)+b,其中A>0,ω>0,0<φ<π.