题目内容
如图，已知P是矩形ABCD内任意一点，延长BP交AD于E，延长DP交AB于F，延长CP交矩形的外接圆于G．求证：GE⊥GF．考点：与圆有关的比例线段
专题：直线与圆
分析：设CG交AD于Q，延长DF、CB交于R，由已知条件利用三角形相似推导出
=
，
=
，从而得到
=
，推导出△FBG∽△EDG，由此能够证明GE⊥GF．
| AF |
| FB |
| BC |
| BR |
| BC |
| BR |
| QE |
| ED |
| AF |
| FB |
| QE |
| ED |
解答：
证明：设CG交AD于Q，
∵∠GBA=∠GDA，∠AGB=∠CGD，
∴△ABG∽△QDG，
延长DF、CB交于R，
∵ABCD是矩形，∴AD∥BC，∴AD∥BR，AD=BC
∴
=
①
又∵RC∥AD，∴△CPB∽△QPE，△RPB∽△DPE，
∴
=
，②
由①，②得
=
，
∵F，E是△ABG，△QDG的相似对应点，
∴△FBG∽△EDG，
∴∠FGB=∠EGD，∠FGE=∠BGD=90°，
∴GE⊥GF．
∵∠GBA=∠GDA，∠AGB=∠CGD，
∴△ABG∽△QDG，
延长DF、CB交于R，
∵ABCD是矩形，∴AD∥BC，∴AD∥BR，AD=BC
∴
| AF |
| FB |
| BC |
| BR |
又∵RC∥AD，∴△CPB∽△QPE，△RPB∽△DPE，
∴
| BC |
| BR |
| QE |
| ED |
由①，②得
| AF |
| FB |
| QE |
| ED |
∵F，E是△ABG，△QDG的相似对应点，
∴△FBG∽△EDG，
∴∠FGB=∠EGD，∠FGE=∠BGD=90°，
∴GE⊥GF．
点评：本题考查直线垂直的证明，是中档题，解题时要注意三角形相似的证明与应用．
练习册系列答案
科学实验活动册系列答案
相关题目
已知x+y+4＞3x+y-2＞0，若x-y＜λ恒成立，则λ取值范围是（ ）
| A、[9，+∞） |
| B、（9，+∞） |
| C、[10，+∞） |
| D、（10，+∞） |
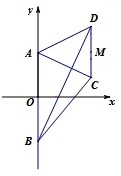如图，梯形ABCD的底边AB在y轴上，原点O为AB的中点，|AB|=